题目内容
某校高三年级有12个班，每个班随机的按1～50号排学号，为了了解某项情况，要求每班学号为20的同学去开座谈会，这里运用的是（ ）
| A、抽签 | B、随机数表法 |
| C、系统抽样法 | D、以上都不是 |
考点：系统抽样方法
专题：操作型,概率与统计
分析：当总体容量N较大时，采用系统抽样．将总体分段，分段的间隔要求相等，这时间隔一般为预先制定的，在第1段内采用简单随机抽样确定一个起始编号，在此编号的基础上加上分段间隔的整倍数即为抽样编号．
解答：
解：本题中，把每个班级学生从1到50号编排，要求每班学号为20的同学去开座谈会，这样选出的样本是采用系统抽样的方法，
故选：C．
故选：C．
点评：本题考查系统抽样，当总体容量N较大时，采用系统抽样，将总体分成均衡的若干部分即将总体分段，分段的间隔要求相等，系统抽样又称等距抽样．
练习册系列答案
阅读快车系列答案
相关题目
设a=40.1，b=log40.1，c=0.40.1，则（ ）
| A、a＞b＞c |
| B、b＞a＞c |
| C、a＞c＞b |
| D、b＞c＞a |
设A={y|y=log2x，x＞1}，B={-2，-1，1，2}则下列结论正确的是（ ）
| A、A∩B={-2，-1} |
| B、（∁RA）∪B=（-∞，0） |
| C、A∪B=（0，+∞） |
| D、（∁RA）∩B={-2，-1} |
下列各组命题中，满足“p或q为真”，且“非p为真”的是（ ）
| A、p：0=∅；q：0∈∅ | ||||
| B、p：在△ABC中，若cos2A=cos2B，则A=B；q：y=sinx在第一象限是增函数 | ||||
C、p：a+b≥2
| ||||
D、p：圆（x-1）2+（y-2）2=1的面积被直线|x|=1平分；q：椭圆
|
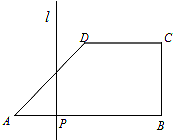在直角梯形ABCD中，AB∥DC，AB⊥BC，且AB=4，BC=CD=2，点P为线段AB上的一动点，过点P作直线l⊥AB，令AP=x，记梯形位于直线l左侧部分的面积S=f（x）．