题目内容
(1)计算:(124+22
)
-27
+16
-2×(8 -
)-1;
(2)
.
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| 4 |
| 2 |
| 3 |
(2)
| ||||||
| lg0.3•lg1.2 |
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)利用指数幂的运算法则即可得出;
(2)利用对数的运算法则即可得出.
(2)利用对数的运算法则即可得出.
解答:
解:(1)原式=[(11+
)2]
-33×
+24×
-2×(23×(-
))-1
=11+
-
+23-2×24
=11+
-
+8-8
=11.
(2)原式=
=
=-
.
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| 4 |
| 2 |
| 3 |
=11+
| 3 |
| 3 |
=11+
| 3 |
| 3 |
=11.
(2)原式=
| ||||||
lg
|
=
(1-lg3)•
| ||
| (lg3-1)(lg3+2lg2-1) |
=-
| 3 |
| 2 |
点评:本题考查了指数幂的运算法则、对数的运算法则,考查了计算能力,属于基础题.

练习册系列答案
相关题目
下列各组命题中,满足“p或q为真”,且“非p为真”的是( )
| A、p:0=∅;q:0∈∅ | ||||
| B、p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数 | ||||
C、p:a+b≥2
| ||||
D、p:圆(x-1)2+(y-2)2=1的面积被直线|x|=1平分;q:椭圆
|
函数y=-
的大致图象是( )
| 1 |
| x+1 |
A、 |
B、 |
C、 |
D、 |
下列式子一定成立的是( )
| A、P(B|A)=P(A|B) |
| B、P(AB)=P(A|B)•P(B)=P(B|A)•P(A) |
| C、0<P(A|B)<1 |
| D、P(A∩B|A)=P(B) |
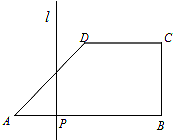 在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).
在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).