题目内容
已知函数f(x)=asinx+bcosx+5(ab≠0)且f(9)=27,则f(-9)= .
考点:两角和与差的正弦函数
专题:计算题,函数的性质及应用
分析:此式可以写成f(x)=
sin(x+q)+5,q是常数.令g(x)=
sin(x+q),即有,g(-9)+g(9)=0.从而可得f(-9)=-17.
| a2+b2 |
| a2+b2 |
解答:
解:此式可以写成f(x)=
sin(x+q)+5,q是常数.
令g(x)=
sin(x+q)
把x+q当成一整体,g(x)显然是奇函数.有g(-x)=-g(x).
即有,g(-9)+g(9)=0.⇒f(-9)-5+f(9)-5=0⇒f(-9)+17=0⇒f(-9)=-17.
故答案为:-17.
| a2+b2 |
令g(x)=
| a2+b2 |
把x+q当成一整体,g(x)显然是奇函数.有g(-x)=-g(x).
即有,g(-9)+g(9)=0.⇒f(-9)-5+f(9)-5=0⇒f(-9)+17=0⇒f(-9)=-17.
故答案为:-17.
点评:本题主要考察了两角和与差的正弦函数,奇函数的性质,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
”a<0”是”函数f(x)=|x(x-2a)|在区间(0,+∞)上单调递增”的( )
| A、必要不充分条件 |
| B、充要条件 |
| C、既不充分也不必要条件 |
| D、充分不必要条件 |
下列式子一定成立的是( )
| A、P(B|A)=P(A|B) |
| B、P(AB)=P(A|B)•P(B)=P(B|A)•P(A) |
| C、0<P(A|B)<1 |
| D、P(A∩B|A)=P(B) |
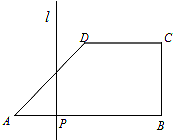 在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).
在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).