题目内容
设全集为R,函数f(x)=
的定义域为M,则∁RM= .
| 1-x2 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据题意,先求出f(x)的定义域M,再求∁RM.
解答:
解:∵f(x)=
,
∴1-x2≥0;
解得-1≤x≤1,
∴f(x)的定义域M=[-1,1],
∴∁RM=(-∞,-1)∪(1,+∞).
故答案为:(-∞,-1)∪(1,+∞).
| 1-x2 |
∴1-x2≥0;
解得-1≤x≤1,
∴f(x)的定义域M=[-1,1],
∴∁RM=(-∞,-1)∪(1,+∞).
故答案为:(-∞,-1)∪(1,+∞).
点评:本题考查了函数定义域的应用问题,解题时应根据函数的解析式求出使解析式有意义的自变量的取值范围即定义域,是基础题.

练习册系列答案
相关题目
设f(x)是[-1,1]上的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(-
)=( )
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知函数f(3x+1)=x2+3x+2,则f(4)=( )
| A、30 | B、6 | C、210 | D、9 |
已知函数f(x)=ax2+bx+c (ac≠0),若f(x)<0的解集为(-1,m),则下列说法正确的是( )
| A、f(m-1)<0 |
| B、f(m-1)>0 |
| C、f(m-1)必与m同号 |
| D、f(m-1)必与m异号 |
设直线l∥平面α,若两直线夹在l与α间的线段相等,则此两条直线必( )
| A、平行 | B、相交 |
| C、异面 | D、平行、相交或异面 |
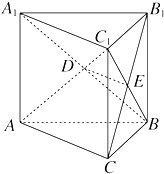 如图所示,直三棱柱ABC-A1B1C1的侧棱长和底面边长都是a,截面AB1C和截面A1BC1相交于DE,求四面体B-B1DE的体积.
如图所示,直三棱柱ABC-A1B1C1的侧棱长和底面边长都是a,截面AB1C和截面A1BC1相交于DE,求四面体B-B1DE的体积.