题目内容
已知函数f(x)=ax2+bx+c (ac≠0),若f(x)<0的解集为(-1,m),则下列说法正确的是( )
| A、f(m-1)<0 |
| B、f(m-1)>0 |
| C、f(m-1)必与m同号 |
| D、f(m-1)必与m异号 |
考点:一元二次不等式的解法
专题:函数的性质及应用,不等式的解法及应用
分析:由于f(x)<0的解集为(-1,m),可得-1,m是一元二次方程ax2+bx+c=0(ac≠0)的两个实数根,且a>0.于是f(x)=a(x+1)(x-m).可得f(m-1)=-am,即可判断出.
解答:
解:∵f(x)<0的解集为(-1,m),
∴-1,m是一元二次方程ax2+bx+c=0(ac≠0)的两个实数根,且a>0.
∴f(x)=a(x+1)(x-m).
∴f(m-1)=-am与m必异号.
故选:D.
∴-1,m是一元二次方程ax2+bx+c=0(ac≠0)的两个实数根,且a>0.
∴f(x)=a(x+1)(x-m).
∴f(m-1)=-am与m必异号.
故选:D.
点评:本题考查了一元二次不等式的解集与相应的一元二次方程的实数根之间的关系,考查了推理能力,属于中档题.

练习册系列答案
相关题目
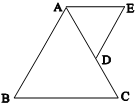 如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,
如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,| BD |
| CE |
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
等差数列{an}中,a1=3,a3=9,若ak=243,则k等于( )
| A、79 | B、80 | C、81 | D、82 |
双曲线4x2-3y2=12的焦距等于( )
| A、2 | ||
| B、4 | ||
C、
| ||
D、2
|