题目内容
17.已知二次函数f(x)=ax2+bx+1(其中b>0)的图象过点(1,4),且其值域为[0,+∞).(1)求f(x)的解析式;
(2)若g(x)=f(x)-kx在区间[-2,2]上是单调函数,求k的取值范围.
分析 (1)由题意可得f(1)=4,判别式为0,解方程可得a=1,b=2,进而得到函数的解析式;
(2)求出g(x)的对称轴,讨论区间[-2,2]为增区间和减区间,解不等式可得k的范围.
解答 解:(1)由题意可得f(1)=4,
即为a+b+1=4,即a+b=3,
由值域为[0,+∞),可得△=b2-4a=0,
解得a=1,b=2,(负的舍去),
则f(x)=x2+2x+1;
(2)g(x)=f(x)-kx=x2+(2-k)x+1,
对称轴为x=$\frac{k-2}{2}$,
若在区间[-2,2]上是单调递增函数,
可得$\frac{k-2}{2}$≤-2,解得k≤-2;
若在区间[-2,2]上是单调递减函数,
可得$\frac{k-2}{2}$≥2,解得k≥6.
即有k的范围是(-∞,-2]∪[6,+∞).
点评 本题考查函数的解析式的求法,注意运用二次函数的值域,考查函数的单调性的运用,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
8. 《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:
《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:
(Ⅰ)在表中作出这些数据的频率分布直方图;
(Ⅱ)已知样本中年龄在[55,65]内的6位选手中,有4名女选手,2名男选手,现从中选3人进行回访,记选出的女选手的人数为X,求X的分布列、数学期望与方差.
 《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:
《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:| 选手年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 频数 | 6 | 22 | 32 | 24 | 10 | 6 |
(Ⅱ)已知样本中年龄在[55,65]内的6位选手中,有4名女选手,2名男选手,现从中选3人进行回访,记选出的女选手的人数为X,求X的分布列、数学期望与方差.
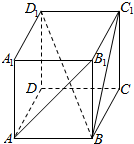 如图,在正方体ABCD-A1B1C1D1中.求:
如图,在正方体ABCD-A1B1C1D1中.求: