题目内容
《九章算术》之后，人们进一步用等差数列求和公式来解决更多的问题，《张丘建算经》卷上第22题为：“今有女善织，日益功疾（注：从第2天开始，每天比前一天多织相同量的布），第一天织5尺布，现在一月（按30天计），共织390尺布”，则从第2天起每天比前一天多织（ ）尺布．
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：利用等差数列的前n项和公式求解．
解答：
解：设从第2天起每天比前一天多织d尺布m
则由题意知30×5+
d=390，
解得d=
．
故选：D．
则由题意知30×5+
| 30×29 |
| 2 |
解得d=
| 16 |
| 29 |
故选：D．
点评：本题考查等差数列的公差的求法，是基础题，解题时要认真审题，注意等差数列的通项公式的求解．
练习册系列答案
相关题目
若存在过点（1，1）的直线与曲线y=x2+x和y=ax2-x-1都相切，则a等于（ ）
| A、-1或-3 | B、-2或3 |
| C、-1或3 | D、1或-3 |
若tanθ=
，则2cos2θ-sin（2θ-π）的值为（ ）
| 1 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设随机变量ξ服从正态分布N（3，4），若P（ξ＜2a-2）=P（ξ＞a+2），则a=（ ）
| A、4 | B、3 | C、2 | D、1 |
三人相互传球，由甲开始发球，经过5次传球后，球仍回到甲手中，则不同的传球方法的种数是（ ）
| A、6 | B、8 | C、10 | D、16 |
已知函数f（x）=|x+a|（a∈R）在[-1，1]上的最大值为M（a），则函数g（x）=M（x）-|x2-1|的零点的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
已知全集U={1，2，3，4，5，6}，集合M={2，3，5}，N={4，5}，则∁U（M∪N）的元素个数有（ ）
| A、0个 | B、1个 | C、2 | D、3个 |
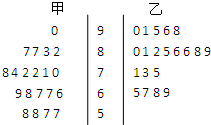为了研究“教学方式”对教学质量的影响，某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）．如图所示茎叶图为甲、乙两班（每班均为20人）学生的数学期末考试成绩．