题目内容
已知全集U={1，2，3，4，5，6}，集合M={2，3，5}，N={4，5}，则∁U（M∪N）的元素个数有（ ）
| A、0个 | B、1个 | C、2 | D、3个 |
考点：交、并、补集的混合运算
专题：集合
分析：先求出M∪N，再求∴∁U（M∪N），由此能求出∁U（M∪N）的元素个数．
解答：
解：∵全集U={1，2，3，4，5，6}，集合M={2，3，5}，N={4，5}，
∴M∪N={2，3，4，5}，
∴∁U（M∪N）={1，6}，
∴∁U（M∪N）的元素个数是2个．
故选：C．
∴M∪N={2，3，4，5}，
∴∁U（M∪N）={1，6}，
∴∁U（M∪N）的元素个数是2个．
故选：C．
点评：本题考查集合中元素个数的求法，是基础题，解题时要认真审题，注意集合的交、并、补集的混合运算．
练习册系列答案
相关题目
设a，b，c分别是△ABC中角A，B，C的对边边长，且lgsinA，lgsinB，lgsinC成等差数列，则直线l1：xsin2A+ysinA-a=0与直线l2：xsin2B+ysinC-c=0的位置关系是（ ）
| A、平行 | B、重合 |
| C、垂直 | D、相交但不垂直 |
《九章算术》之后，人们进一步用等差数列求和公式来解决更多的问题，《张丘建算经》卷上第22题为：“今有女善织，日益功疾（注：从第2天开始，每天比前一天多织相同量的布），第一天织5尺布，现在一月（按30天计），共织390尺布”，则从第2天起每天比前一天多织（ ）尺布．
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）对任意的实数x，都有f（2+x）=f（2-x），f（1+x）=-f（x），且f（x）不恒为0，则f（x）是（ ）
| A、奇函数但非偶函数 |
| B、偶函数但非奇函数 |
| C、既是奇函数又是偶函数 |
| D、是非奇非偶函数 |
下列四个函数中，既是定义域上的奇函数又在区间（0，1）内单调递增的是（ ）
A、y=
| ||
| B、y=xsinx | ||
C、y=lg
| ||
| D、y=ex-e-x |
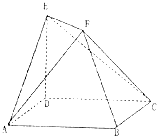如图，底面ABCD是边长为4的正方形，ED⊥平面ABCD，ED=2，EF∥BD，且2EF=BD．