题目内容
已知函数f(x)=|x+a|(a∈R)在[-1,1]上的最大值为M(a),则函数g(x)=M(x)-|x2-1|的零点的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:求出M(a)的解析式,根据函数g(x)=M(x)-|x2-1|的零点,即函数M(x)=
与函数y=|x2-1|交点的横坐标,利用图象法解答.
|
解答:
解:∵函数f(x)=|x+a|(a∈R)在[-1,1]上的最大值为M(a),
∴M(a)=
,
函数g(x)=M(x)-|x2-1|的零点,
即函数M(x)=
与函数y=|x2-1|交点的横坐标,

由图可得:函数M(x)=
与函数y=|x2-1|有三个交点,
故函数g(x)=M(x)-|x2-1|有3个零点,
故选:C
∴M(a)=
|
函数g(x)=M(x)-|x2-1|的零点,
即函数M(x)=
|

由图可得:函数M(x)=
|
故函数g(x)=M(x)-|x2-1|有3个零点,
故选:C
点评:本题考查函数图象的作法,熟练作出函数的图象是解决问题的关键,属中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
复数
的共轭复数是( )
| i+1 |
| 1-i |
| A、2 | B、i | C、-i | D、-2i |
直线l1过点A(2,-1)和点B(3,2),直线l2的倾斜角是直线l1的倾斜角的两倍,则直线l2的斜率为( )
| A、-6 | ||
B、-
| ||
C、
| ||
D、-
|
《九章算术》之后,人们进一步用等差数列求和公式来解决更多的问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一天织5尺布,现在一月(按30天计),共织390尺布”,则从第2天起每天比前一天多织( )尺布.
A、
| ||
B、
| ||
C、
| ||
D、
|
已知m,n∈R则“m>0且n>0”是“曲线
+
=1为椭圆”的( )
| x2 |
| m |
| y2 |
| n |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数f(x)对任意的实数x,都有f(2+x)=f(2-x),f(1+x)=-f(x),且f(x)不恒为0,则f(x)是( )
| A、奇函数但非偶函数 |
| B、偶函数但非奇函数 |
| C、既是奇函数又是偶函数 |
| D、是非奇非偶函数 |
下列四个函数中,既是定义域上的奇函数又在区间(0,1)内单调递增的是( )
A、y=
| ||
| B、y=xsinx | ||
C、y=lg
| ||
| D、y=ex-e-x |
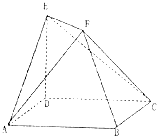 如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF∥BD,且2EF=BD.
如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF∥BD,且2EF=BD.