题目内容
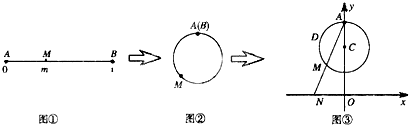
下图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.
给出下列命题:①f(
)=1;
②f(
)=0;
③f(x)是奇函数;
④f(x)在定义域上单调递增,
则所有真命题的序号是( )
给出下列命题:①f(
| 1 |
| 4 |
②f(
| 1 |
| 2 |
③f(x)是奇函数;
④f(x)在定义域上单调递增,
则所有真命题的序号是( )

| A、①② | B、②③ | C、①④ | D、②④ |
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用
分析:由题中对映射运算描述,对四个命题逐一判断其真伪,
①m=
此时M恰好处在左半圆弧的中点上,求出直线AM的方程后易得N的横坐标;
②当m=
时,对应的点在点A的正下方,即可求出n;
③可由奇函数的定义域关于原点对称来确定正误;
④可由图3,由M的运动规律观察出函数值的变化,得出单调性.
①m=
| 1 |
| 4 |
②当m=
| 1 |
| 2 |
③可由奇函数的定义域关于原点对称来确定正误;
④可由图3,由M的运动规律观察出函数值的变化,得出单调性.
解答:
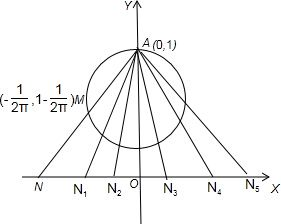 解:如图,因为M在以(1,1-
解:如图,因为M在以(1,1-
)为圆心,
为半径的圆上运动,
对于①当m=
时.M的坐标为(-
,1-
),
直线AM方程y=x+1,所以点N的坐标为(-1,0),
故f(
)=-1,则①错;
对于②,当m=
时,对应的点在点A的正下方,
此时点N(0,0),所以f(
)=0,则②对;
对于③,因为实数m所在区间(0,1)不关于原点对称,所以f(x)不存在奇偶性.则③错;
对于④,当实数m越来越大时,
如图直线AM与x轴的交点N(n,0)也越来越往右,
即n也越来越大,所以f(x)在定义域上单调递增,则④对.
其中正确的为②④.
故选D.
 解:如图,因为M在以(1,1-
解:如图,因为M在以(1,1-| 1 |
| 2π |
| 1 |
| 2π |
对于①当m=
| 1 |
| 4 |
| 1 |
| 2π |
| 1 |
| 2π |
直线AM方程y=x+1,所以点N的坐标为(-1,0),
故f(
| 1 |
| 4 |
对于②,当m=
| 1 |
| 2 |
此时点N(0,0),所以f(
| 1 |
| 2 |
对于③,因为实数m所在区间(0,1)不关于原点对称,所以f(x)不存在奇偶性.则③错;
对于④,当实数m越来越大时,
如图直线AM与x轴的交点N(n,0)也越来越往右,
即n也越来越大,所以f(x)在定义域上单调递增,则④对.
其中正确的为②④.
故选D.
点评:本题考查映射的概念,解答本题关键是理解题设中所给的对应关系,正确认识三个图象的意义,由此对四个命题的正误作出判断,本题题型新颖,寓数于形,是一个考查理解能力的题,对题设中所给的关系进行探究,方可得出正确答案,本题易因为理解不了题意而导致无法下手,题目较抽象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题p:?x∈R,x2+x-1<0,则¬p为( )
| A、?x∈R,x2+x-1>0 |
| B、?x∈R,x2+x-1≥0 |
| C、?x∉R,x2+x-1≥0 |
| D、?x∉R,x2+x-1>0 |
直线x+my+1=0与不等式组
表示的平面区域有公共点,则实数m的取值范围是( )
|
A、[
| ||||
B、[-
| ||||
C、[
| ||||
D、[-3,-
|
函数y=
+
的定义域为( )
| 1-x |
| x |
| A、{x|x≤1} |
| B、{x|x≥0} |
| C、{x|x≥1或x≤0} |
| D、{x|0≤x≤1} |
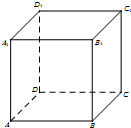 已知正方体ABCD-A1B1C1D1的棱长为1.给出下列五个命题:
已知正方体ABCD-A1B1C1D1的棱长为1.给出下列五个命题: