题目内容
函数y=
+
的定义域为（ ）
| 1-x |
| x |
| A、{x|x≤1} |
| B、{x|x≥0} |
| C、{x|x≥1或x≤0} |
| D、{x|0≤x≤1} |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：保证两个根式都有意义的自变量x的集合为函数的定义域．
解答：
解：要使原函数有意义，则需
，
解得0≤x≤1，
所以，原函数定义域为[0，1]．
故选：D．
|
解得0≤x≤1，
所以，原函数定义域为[0，1]．
故选：D．
点评：本题考查了函数定义域的求法，求解函数的定义域，是求使的构成函数解析式的各个部分都有意义的自变量x的取值集合．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
下列函数中，表示同一函数的一组是（ ）
A、f（x）=
| |||||||
| B、f（x）=lg（x（x+1）），g（x）=lgx+lg（x+1） | |||||||
| C、f（x）=x-1（x∈R），g（x）=x-1（x∈N） | |||||||
| D、f（x）=x2+x-1，g（x）=t2+t-1 |
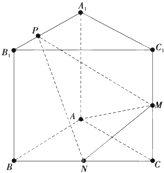如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=2，AB⊥AC，M、N分别是CC1、BC的中点，点P在线段A1B1上，且
在直角坐标系中，点A，B，C的坐标分别为(0，1)，(
，0)，(0，-2)，O为坐标原点，动点P满足|
|=1，则|
+
+
|的最小值是（ ）
| 2 |
| CP |
| OA |
| OB |
| OP |
A、4-2
| ||
B、
| ||
C、
| ||
D、
|