题目内容
已知A，B分别是椭圆x2+4y2=4与圆x2+（y-2）2=1上的点，求AB的最大值．
考点：圆与圆的位置关系及其判定
专题：圆锥曲线中的最值与范围问题
分析：用参数方程，设出椭圆上的点A的坐标，求出点A到圆心C（0，2）的距离的最大值，从而得出AB的最大值．
解答：
解：∵A，B分别是椭圆x2+4y2=4与圆x2+（y-2）2=1上的点，
∴椭圆的标准方程为
+y2=1，
设椭圆上的点A（2cosθ，sinθ），θ∈[0，2π）；
则点A到圆心C（0，2）的距离为
d=
=
=
，
当sinθ=-
时，d取得最大值为
=
，
∴AB的最大值为
+1．
∴椭圆的标准方程为
| x2 |
| 4 |
设椭圆上的点A（2cosθ，sinθ），θ∈[0，2π）；
则点A到圆心C（0，2）的距离为
d=
| (2cosθ)2+(sinθ-2)2 |
=
| 4cos2θ+sin2θ-4sinθ+4 |
=
-3(sinθ+
|
当sinθ=-
| 2 |
| 3 |
|
| 2 |
| 3 |
| 21 |
∴AB的最大值为
| 2 |
| 3 |
| 21 |
点评：本题考查了椭圆与圆的方程以及距离的最值的应用问题，也考查了参数方程的应用问题，是中档题目．
练习册系列答案
相关题目
函数f（x）=lg（x-1）的定义域为（ ）
| A、（0，+∞） |
| B、（-∞，0） |
| C、（1，+∞） |
| D、（-∞，1） |
在△OAB中，|
|=a，|
|=b，OD是AB边上的高，若
=λ
，则实数λ等于（ ）
| OA |
| OB |
| AD |
| AB |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
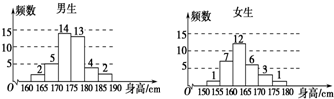为了解学生身高情况，某校以10%的比例对高三年级的700名学生按性别进行分层抽样调查，测得身高情况的统计图如图：