题目内容
19．已知a，b，c为正实数，且a+b≤6c，$\frac{2}{a}$+$\frac{3}{b}$≤$\frac{2}{c}$，则$\frac{3a+8b}{c}$的取值范围为（0，48）．分析 利用已知条件化简不等式，画出约束条件的可行域，然后判断目标函数的范围即可．
解答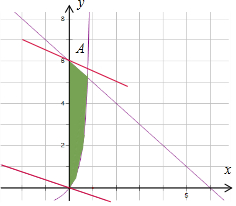 
解：a，b，c为正实数，且a+b≤6c，$\frac{2}{a}$+$\frac{3}{b}$≤$\frac{2}{c}$，
可得$\frac{a}{c}+\frac{b}{c}≤6$，$\frac{2c}{a}+\frac{3c}{b}≤2$，令$x=\frac{a}{c}$，y=$\frac{b}{c}$，
不等式化简为：$\left\{\begin{array}{l}{x＞0}\\{y＞0}\\{x+y≤6}\\{\frac{2}{x}+\frac{3}{y}≤2}\end{array}\right.$，
则z=$\frac{3a+8b}{c}$化为：z=3x+8y，
画出不等式组的可行域如图：
z=3x+8y如图中的红色直线，当z经过原点与a时，分别取得最小值与最大值，
所以3x+8y的最小值为：0，最大值为：48．
所以$\frac{3a+8b}{c}$的取值范围为：（0，48）．
故答案为：（0，48）
点评 本题考查线性规划的简单应用，考查数形结合以及转化思想的应用．
练习册系列答案
相关题目
7．已知O为原点，当θ=-$\frac{π}{6}$时，参数方程$\left\{\begin{array}{l}{x=3cosθ}\\{y=9sinθ}\end{array}\right.$（θ为参数）上的点为A，则直线OA的倾斜角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
我国的《洛书》中记载着世界上最古老的幻方：将1，2，…，9填入方格内，使三行、三列，两条对角线的三个数之和都等于15，如图所示．
11．在同一坐标系中，将曲线y=$\frac{1}{2}$sin3x变为曲线y'=sinx′的伸缩变换是（ ）
| A． | $\left\{{\begin{array}{l}{x=3x'}\\{y=\frac{1}{2}y'}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{x'=3x}\\{y'=\frac{1}{2}y}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{x=3x'}\\{y=2y'}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{x'=3x}\\{y'=2y}\end{array}}\right.$ |