题目内容
7.已知O为原点,当θ=-$\frac{π}{6}$时,参数方程$\left\{\begin{array}{l}{x=3cosθ}\\{y=9sinθ}\end{array}\right.$(θ为参数)上的点为A,则直线OA的倾斜角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 求出A点坐标,计算直线OA的斜率,从而得出倾斜角的大小.
解答 解:A点坐标为($\frac{3\sqrt{3}}{2}$,-$\frac{9}{2}$),
∴直线OA的斜率k=-$\sqrt{3}$,
∴直线OA的倾斜角为$\frac{2π}{3}$.
故选C.
点评 本题考查了直线的参数方程,直线的一般方程,属于基础题.

练习册系列答案
相关题目
15.记凸n(n≥3)边形的对角线的条数为f(n),则f(n)的表达式为( )
| A. | f(n)=n+1 | B. | f(n)=2n-1 | C. | $f(n)=\frac{{n({n-3})}}{2}$ | D. | $f(n)=\frac{{n({n+1})}}{2}$ |
12.若某空间几何体的三视图如图所示,则该几何体的表面积是( )
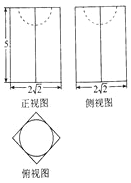

| A. | 48+π | B. | 48-π | C. | 48+2π | D. | 48-2π |