球和它的内接正方体的表面积之比是$\frac{π}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

9．球和它的内接正方体的表面积之比是$\frac{π}{2}$．

分析根据球的直径与正方体体对角线相等得出棱长与半径的关系，代入面积公式计算即可．

解答解：设正方体棱长为a，则球的半径r=$\frac{\sqrt{3}a}{2}$，
∴S_球=4πr²=3πa²，S_正方体=6a²，
∴$\frac{{S}_{球}}{{S}_{正方体}}$=$\frac{3π{a}^{2}}{6{a}^{2}}$=$\frac{π}{2}$．
故答案为：$\frac{π}{2}$．

点评本题考查了球与内接正方体的位置关系，几何体的表面积计算，属于基础题．

练习册系列答案

世纪百通主体课堂小学课时同步达标系列答案

20．定义在R上的函数f（x）满足：①f（-x）=-f（x）；②f（2x）=af（x）（a＞0）；③当2≤x≤4时，$f（x）=|sin\frac{π}{2}x|$，若分别以函数f（x）的极值点和相应极值为横、纵坐标的点都在一条直线上，则a的值为（　　）

17．在△ABC中，M是线段AB的中点，$\overrightarrow{AN}=\frac{1}{2}\overrightarrow{NC}$，BN与CM相交于点E，设$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，
（1）用基底$\vec a$，$\vec b$表示$\overrightarrow{BN}$和$\overrightarrow{CM}$；
（2）用基底$\vec a$，$\vec b$表示$\overrightarrow{AE}$．

4．在平面直角坐标系xoy中，曲线C₁的参数方程为$\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=-2+\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数），以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C₂的极坐标方程为ρ²（1+sin²θ）=8．
（1）求曲线C₁和C₂的普通方程；
（2）若曲线C₁和C₂交于两点A，B，求|AB|的值．

14．观察下列数表：
2
4，6
8，10，12，14
16，18，20，22，24，26，28，30
…
设2016是该表第m行的第n个数，则m+n=507．

1．网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（　　）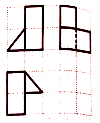

A．

B．

C．

$\frac{2\sqrt{2}}{3}$

D．

1+$\frac{2\sqrt{2}}{3}$

18．在极坐标系中，点$A（3，\frac{5π}{12}）$与点$B（8，\frac{π}{12}）$之间的距离等于7．

19．在直角坐标系xOy中，圆C的参数方程为$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$（φ为参数），直线l的方程为x+$\sqrt{3}$y-9=0，以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求圆C和直线l的极坐标方程；
（2）射线OA：θ=$\frac{π}{6}$与圆C的交点是O，M，与直线l的交点为N，求线段MN的长．

试题分类