题目内容

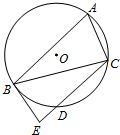如图，A，B，C是⊙O上的三点，BE切⊙O于点B，D是CE与⊙O的交点．若∠BAC=60°，BC=2BE，求证：CD=2ED．
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：利用圆的切线的性质，结合BC=2BE，可得∠BEC=90°，则EC=
3
BE，利用切割线定理，可得ED=
3
3
BE，从而可得CD，即可证明结论．
解答： 证明：因为BE切⊙O于点B，
所以∠CBE=∠BAC=60°，
因为BC=2BE，
所以∠BEC=90°，则EC=
3
BE．
又因为BE2=EC•ED，
所以ED=
3
3
BE，
所以CD=
2
3
3
BE．
即CD=2ED．
点评：本题考查圆的切线的性质、切割线定理，考查学生分析解决问题的能力，正确运用切割线定理是关键．
练习册系列答案
相关题目
已知a，b，c为△ABC的三边，若b2+c2-a2=bc，则
b+c
a
的取值范围是（　　）
A、（1，2]
B、（1，
3
]
C、[
3
，2]
D、（
3
，2]
在平面直角坐标系中，记由点A（0，1），B（4，2），C（2，6）围成的三角形区域（含边界）为D，P（x，y）为区域D上的点，则
(x-2)2+(y-2)2
最大值与最小值的和为（　　）
A、
4
5
5
B、
4
5
5
+
2
17
17
C、4
D、
2
17
17
+4
已知等比数列{an}的前n项和为Sn，且满足
S6
S3
=9，则公比q=（　　）
A、
1
2
B、±
1
2
C、2
D、±2
数列{an}满足a1=0，a2=2，an+2=（1+cos2
nπ
2
）an+4sin2
nπ
2
，n=1，2，3，…，
（1）求a3，a4，a5，a6；
（2）设Sk=a1+a3+…+a2k-1，Tk=a2+a4+…+a2k，分别求Sk，Tk关于k的表达式；
（3）设Wk=
2Sk
2+Tk
，求使Wk＞1的所有k的值，并说明理由．
设
a
，
a
，
b
为向量，若
a
+
b
与
a
的夹角为
π
3
，
a
+
b
与
b
的夹角为
π
4
，则
|
a
|
|
b
|
=
 
．
在△ABC中，内角A，B，C所对边长分别为a，b，c，tanB=
4
3
，sinA=
5
13
．
（Ⅰ）求cosC；
（Ⅱ）若△ABC的面积是1，求
AB
•
AC
．
已知函数f（x）=-x3+x2+b，g（x）=alnx．
（1）若f（x）的极大值为
4
27
，求实数b的值；
（2）若对任意x∈[1，e]，都有g（x）≥-x2+（a+2）x恒成立，求实数a的取值范围；
（3）若函数f（x）满足：在定义域内存在实数x0，使f（x0+k）=f（x0）+f（k）（k为常数），则称“f（x）关于k可线性分解”．设b=0，若F（x）=
af(x)
x2
+g（x）关于实数a可线性分解，求a取值范围．
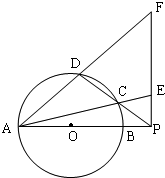如图，圆O的直径AB=10，P是AB延长线上一点，BP=2，割线PCD交圆O于点C，D，过点P做AP的垂线，交直线AC于点E，交直线AD于点F．
（1）求证：∠PEC=∠PDF；
（2）求PE•PF的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网