题目内容
已知a,b,c为△ABC的三边,若b2+c2-a2=bc,则
的取值范围是( )
| b+c |
| a |
| A、(1,2] | ||
B、(1,
| ||
C、[
| ||
D、(
|
考点:余弦定理
专题:三角函数的求值
分析:利用余弦定理表示出cosA,将已知等式代入计算求出cosA的值,确定出A的度数,进而求出B+C的度数,用B表示出C,所求式子利用正弦定理化简,将sinA的值与表示出的C代入,利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域即可确定出范围.
解答:
解:∵△ABC中,b2+c2-a2=bc,
∴cosA=
=
=
,
∴A=60°,即B+C=120°,
将
利用正弦定理化简得:
=
=
[sinB+sin(120°-B)]=
(
sinB+
cosB)=2(
sinB+
cosB)=2sin(B+30°),
∵0<B<120°,即30°<B+30°<150°,
∴
<sin(B+30°)≤1,即1<2sin(B+30°)≤2,
则
的取值范围是(1,2].
故选:A.
∴cosA=
| b2+c2-a2 |
| 2bc |
| bc |
| 2bc |
| 1 |
| 2 |
∴A=60°,即B+C=120°,
将
| b+c |
| a |
| sinB+sinC |
| sinA |
| sinB+sinC | ||||
|
2
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∵0<B<120°,即30°<B+30°<150°,
∴
| 1 |
| 2 |
则
| b+c |
| a |
故选:A.
点评:此题考查了正弦、余弦定理,以及正弦函数的值域,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
已知集合M={x|x2-x≤0},函数f(x)=
的定义域为D,则M∩D=( )
| 1 | ||
|
| A、[0,1) | B、(0,1) |
| C、(0,1] | D、{1} |
已知
=(1,k),
=(k,4),那么“k=-2”是“
,
共线”的( )
| a |
| b |
| a |
| b |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
下列命题中,错误的是( )
| A、平行于同一平面的两个不同平面平行 |
| B、一条直线与两个平行平面中的一个相交,则必与另一个平面相交 |
| C、若直线l与平面α相交但不垂直,则经过该直线l有且只有一个平面β与α垂直 |
| D、若直线l不平行平面α,则在平面α内不存在与l平行的直线 |
复数
在复平面内对应的点位于( )
| 1 |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若θ∈[
,
],sin2θ=
,则cosθ=( )
| π |
| 4 |
| π |
| 2 |
3
| ||
| 8 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
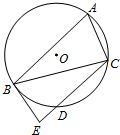 如图,A,B,C是⊙O上的三点,BE切⊙O于点B,D是CE与⊙O的交点.若∠BAC=60°,BC=2BE,求证:CD=2ED.
如图,A,B,C是⊙O上的三点,BE切⊙O于点B,D是CE与⊙O的交点.若∠BAC=60°,BC=2BE,求证:CD=2ED.