题目内容
在平面直角坐标系中，记由点A（0，1），B（4，2），C（2，6）围成的三角形区域（含边界）为D，P（x，y）为区域D上的点，则
最大值与最小值的和为（ ）
| (x-2)2+(y-2)2 |
A、
| ||||||||
B、
| ||||||||
| C、4 | ||||||||
D、
|
考点：简单线性规划
专题：不等式的解法及应用
分析：判断
的几何意义，然后利用可行域求解最大值与最小值的和．
| (x-2)2+(y-2)2 |
解答：
解：
表示区域中的点P（x，y）与点E（2，2）的距离．
①Q点（2，2）是区域中的点，
的最小值为0；
②由区域D可知，
的最大值为|CE|=4，
故选：C．
解：| (x-2)2+(y-2)2 |
①Q点（2，2）是区域中的点，
| (x-2)2+(y-2)2 |
②由区域D可知，
| (x-2)2+(y-2)2 |
故选：C．
点评：本题考查线性规划的解答应用，注意表达式的几何意义是解题的关键，考查计算能力．
练习册系列答案
相关题目
已知集合M={x|x2-x≤0}，函数f（x）=
的定义域为D，则M∩D=（ ）
| 1 | ||
|
| A、[0，1） | B、（0，1） |
| C、（0，1] | D、{1} |
若θ∈[
，
]，sin2θ=
，则cosθ=（ ）
| π |
| 4 |
| π |
| 2 |
3
| ||
| 8 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
A，B两个学生分别从2名数学教师和2名英语教师共4人中各选择一位教师给自己补缺补差，若A，B不选同一位教师，则学生A选择数学教师，学生B选择英语教师的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
等比数列{an}中a4+a8=-2，则a42+2a62+a6a10的值为（ ）
| A、4 | B、5 | C、8 | D、-9 |
在△ABC中，若角A、B、C的对边分别是a、b、c，则“a2+c2=b2+ac”，是“A、B、C依次成等差数列”的（ ）
| A、既不充分也不必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、充要条件 |
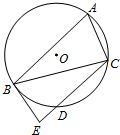如图，A，B，C是⊙O上的三点，BE切⊙O于点B，D是CE与⊙O的交点．若∠BAC=60°，BC=2BE，求证：CD=2ED．
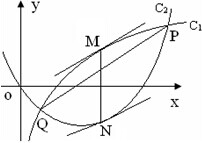已知函数f（x）=lnx，g（x）=