题目内容
数列{an}满足a1=0,a2=2,an+2=(1+cos2
)an+4sin2
,n=1,2,3,…,
(1)求a3,a4,a5,a6;
(2)设Sk=a1+a3+…+a2k-1,Tk=a2+a4+…+a2k,分别求Sk,Tk关于k的表达式;
(3)设Wk=
,求使Wk>1的所有k的值,并说明理由.
| nπ |
| 2 |
| nπ |
| 2 |
(1)求a3,a4,a5,a6;
(2)设Sk=a1+a3+…+a2k-1,Tk=a2+a4+…+a2k,分别求Sk,Tk关于k的表达式;
(3)设Wk=
| 2Sk |
| 2+Tk |
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)根据数列的递推式直接求a3,a4,a5,a6;
(2)根据Sk=a1+a3+…+a2k-1,Tk=a2+a4+…+a2k,即可求Sk,Tk关于k的表达式;
(3)求出Wk=
,解不等式Wk>1即可得到结论.
(2)根据Sk=a1+a3+…+a2k-1,Tk=a2+a4+…+a2k,即可求Sk,Tk关于k的表达式;
(3)求出Wk=
| 2Sk |
| 2+Tk |
解答:
解:(1)∵a1=0,a2=2,
∴a3=(1+cos2
)a1+4sin2
=4,a4=(1+cos2
)a2+4sin2
=4,a5=(1+cos2
)a3+4sin2
=8,a6=(1+cos2
)a4+4sin2
=8.
(2)当n=2k-1(k∈N*)时,a2k+1=(1+cos2
π)a2k-1+4sin2
π=a2k-1+4,
∴{a2k-1}是以0为首项,4为公差的等差数列,则a2k-1=4(k-1),
当n=2k(k∈N*)时,a2k+2=(1+cos2
π)a2k+4sin2
π=2a2k,
∴{a2k}是以2为首项,2为公比的等比数列,则a2k=2k,
∴{an}的通项公式为an=
Sk=a1+a3+…+a2k-1=0+4+…+4(k-1)=2k(k-1),Tk=a2+a4+…+a2k=2+22+…+2k=2k+1-2,
(3)Wk=
=
=
,
于是W1=0,W2=1,W3=
,W4=
,W5=
,W6=
.
下面证明:当k≥6时,Wk<1.
事实上,当k≥6时,Wk+1-Wk=
-
=
<0,即Wk+1<Wk,
又W6<1,∴当k≥6时,Wk<1.
∵W1=0,W2=1,不满足Wk>1
∴满足Wk>1的k的值为3,4,5.
∴a3=(1+cos2
| π |
| 2 |
| π |
| 2 |
| 2π |
| 2 |
| 2π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| 4π |
| 2 |
| 4π |
| 2 |
(2)当n=2k-1(k∈N*)时,a2k+1=(1+cos2
| 2k-1 |
| 2 |
| 2k-1 |
| 2 |
∴{a2k-1}是以0为首项,4为公差的等差数列,则a2k-1=4(k-1),
当n=2k(k∈N*)时,a2k+2=(1+cos2
| 2k |
| 2 |
| 2k |
| 2 |
∴{a2k}是以2为首项,2为公比的等比数列,则a2k=2k,
∴{an}的通项公式为an=
|
Sk=a1+a3+…+a2k-1=0+4+…+4(k-1)=2k(k-1),Tk=a2+a4+…+a2k=2+22+…+2k=2k+1-2,
(3)Wk=
| 2Sk |
| 2+Tk |
| 4k(k-1) |
| 2k+1 |
| k(k-1) |
| 2k-1 |
于是W1=0,W2=1,W3=
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 15 |
| 16 |
下面证明:当k≥6时,Wk<1.
事实上,当k≥6时,Wk+1-Wk=
| (k+1)k |
| 2k |
| k(k-1) |
| 2k-1 |
| k(3-k) |
| 2k |
又W6<1,∴当k≥6时,Wk<1.
∵W1=0,W2=1,不满足Wk>1
∴满足Wk>1的k的值为3,4,5.
点评:本题主要考查数列的应用,要求熟练掌握等比数列和等差数列的相关公式,考查学生的运算能力,综合性较强,运算量较大.

练习册系列答案
相关题目
下列命题中,错误的是( )
| A、平行于同一平面的两个不同平面平行 |
| B、一条直线与两个平行平面中的一个相交,则必与另一个平面相交 |
| C、若直线l与平面α相交但不垂直,则经过该直线l有且只有一个平面β与α垂直 |
| D、若直线l不平行平面α,则在平面α内不存在与l平行的直线 |
等比数列{an}中a4+a8=-2,则a42+2a62+a6a10的值为( )
| A、4 | B、5 | C、8 | D、-9 |
已知(ax+1)5的展开式中x3的系数是10,则实数a的值是( )
| A、1 | ||
B、
| ||
| C、-1 | ||
| D、2 |
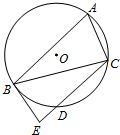 如图,A,B,C是⊙O上的三点,BE切⊙O于点B,D是CE与⊙O的交点.若∠BAC=60°,BC=2BE,求证:CD=2ED.
如图,A,B,C是⊙O上的三点,BE切⊙O于点B,D是CE与⊙O的交点.若∠BAC=60°,BC=2BE,求证:CD=2ED.