题目内容
设
，
，
为向量，若
+
与
的夹角为
，
+
与
的夹角为
，则
= ．
| a |
| a |
| b |
| a |
| b |
| a |
| π |
| 3 |
| a |
| b |
| b |
| π |
| 4 |
|
| ||
|
|
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：利用向量加法的平行四边形法则作图，右图可得相应的角，利用正弦定理可求答案．
解答：
解：如图所示（其中图中字母表示对应向量），
向量
+
与
的夹角为
，
+
与
的夹角为
，
∴∠CAB=
，∠ACB=
，
由正弦定理，得
=
，即
=
，
∴
=
=
，
故答案为：
．
解：如图所示（其中图中字母表示对应向量），向量
| a |
| b |
| a |
| π |
| 3 |
| a |
| b |
| b |
| π |
| 4 |
∴∠CAB=
| π |
| 3 |
| π |
| 4 |
由正弦定理，得
| AB |
| sin∠ACB |
| BC |
| sin∠CAB |
|
| ||
sin
|
|
| ||
sin
|
∴
|
| ||
|
|
| ||||
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查平面向量数量积运算、正弦定理及加法的平行四边形法则，属基础题．
练习册系列答案
相关题目
复数
在复平面内对应的点位于（ ）
| 1 |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中，若角A、B、C的对边分别是a、b、c，则“a2+c2=b2+ac”，是“A、B、C依次成等差数列”的（ ）
| A、既不充分也不必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、充要条件 |
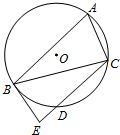如图，A，B，C是⊙O上的三点，BE切⊙O于点B，D是CE与⊙O的交点．若∠BAC=60°，BC=2BE，求证：CD=2ED．