题目内容
在△ABC中，内角A，B，C所对边长分别为a，b，c，tanB=
，sinA=
．
（Ⅰ）求cosC；
（Ⅱ）若△ABC的面积是1，求
•
．
| 4 |
| 3 |
| 5 |
| 13 |
（Ⅰ）求cosC；
（Ⅱ）若△ABC的面积是1，求
| AB |
| AC |
考点：正弦定理的应用,平面向量数量积的运算
专题：综合题,解三角形,平面向量及应用
分析：（Ⅰ）由题设条件先由同角三角函数的基本关系求出角A，B的正弦与余弦值，再由cosC=-cos（A+B）即可可求出角C的余弦值；
（II）由面积公式求出bc的值，再由数量积公式即可求出
•
．
（II）由面积公式求出bc的值，再由数量积公式即可求出
| AB |
| AC |
解答：
解：（Ⅰ）由tanB=
，0＜B＜π，可得sinB=
，cosB=
；…（2分）
sinA=
＜sinB=
，
由正弦定理，a＜b，则A＜B，故0＜A＜
，cosA=
．…（4分）
由A+B+C=π，cosC=-cos（A+B）=sinAsinB-cosAcosB=
×
-
×
=-
．…（6分）
（Ⅱ）由△ABC的面积是1，可得
bcsinA=
bc=1，得bc=
．…（9分）
•
=bccosA=
×
=
．…（12分）
| 4 |
| 3 |
| 4 |
| 5 |
| 3 |
| 5 |
sinA=
| 5 |
| 13 |
| 4 |
| 5 |
由正弦定理，a＜b，则A＜B，故0＜A＜
| π |
| 2 |
| 12 |
| 13 |
由A+B+C=π，cosC=-cos（A+B）=sinAsinB-cosAcosB=
| 5 |
| 13 |
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 16 |
| 56 |
（Ⅱ）由△ABC的面积是1，可得
| 1 |
| 2 |
| 5 |
| 26 |
| 26 |
| 5 |
| AB |
| AC |
| 12 |
| 13 |
| 26 |
| 5 |
| 24 |
| 5 |
点评：本题考查正弦定理的应用，三角形的面积公式，数量积的公式，同角三角函数的基本关系，涉及到的公式较多，知识性强，但难度不高，主要考查知识的运用能力及计算能力
练习册系列答案
阅读快车系列答案
相关题目
若θ∈[
，
]，sin2θ=
，则cosθ=（ ）
| π |
| 4 |
| π |
| 2 |
3
| ||
| 8 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
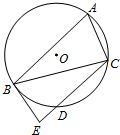如图，A，B，C是⊙O上的三点，BE切⊙O于点B，D是CE与⊙O的交点．若∠BAC=60°，BC=2BE，求证：CD=2ED．
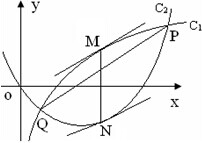已知函数f（x）=lnx，g（x）=