题目内容
已知数列{an}满足递推关系,an+1=
(n∈N*),又a1=1.
(1)当m=1时,求证数列{an+1}为等比数列;
(2)当m在什么范围取值时,能使数列{an}满足不等式an+1≥an恒成立?
(3)当-3≤m<1时,证明:
+
+…+
≥1-
.
| 2an2+3an+m |
| an+1 |
(1)当m=1时,求证数列{an+1}为等比数列;
(2)当m在什么范围取值时,能使数列{an}满足不等式an+1≥an恒成立?
(3)当-3≤m<1时,证明:
| 1 |
| a1+1 |
| 1 |
| a2+1 |
| 1 |
| an+1 |
| 1 |
| 2n |
考点:数列与不等式的综合,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出an+1+1=2(an+1),由此能证明{an+1}是等比数列.
(2)由an+1≥an,得m≥-(an+1)2+1恒成立,由此能推导出当m≥-3时,能使数列{an}满足不等式an+1≥an恒成立.
(3)设cn=
,则cn+1=
=
=
,由此能证明
+
+…+
≥1-
.
(2)由an+1≥an,得m≥-(an+1)2+1恒成立,由此能推导出当m≥-3时,能使数列{an}满足不等式an+1≥an恒成立.
(3)设cn=
| 1 |
| an+1 |
| 1 |
| an+1+1 |
| 1 | ||
|
| an+1 |
| 2(an+1)2+m-1 |
| 1 |
| a1+1 |
| 1 |
| a2+1 |
| 1 |
| an+1 |
| 1 |
| 2n |
解答:
(1)解:由an+1=
=
=2an+1,
得an+1+1=2(an+1),
∵a1+1≠0,
∴{an+1}是等比数列.…(4分)
(2)解:由an+1≥an,a1=1,得an≥1,
∴
≥an,
∴m≥-an2-2an,…(6分)
∴m≥-(an+1)2+1恒成立,
∵an≥1,∴m≥-22+1=-3,
∴当m≥-3时,能使数列{an}满足不等式an+1≥an恒成立.…(9分)
(3)证明:由(2)得当-3≤m<1时,an+1≥an,∴an>0,
设cn=
,
则cn+1=
=
=
,
∵m<1,∴m-1<0,
∴cn+1>
=
=
cn,
∵c1=
=
,
∴cn>
cn-1>
cn-2>…>
c1=
(n≥2),
∴c1+c2+c3+…cn>
+
+
+…
=
=1-
(n≥2),
∴
+
+…+
≥1-
.…(14分)
2
| ||
| an+1 |
| (2an+1)(an+1) |
| an+1 |
得an+1+1=2(an+1),
∵a1+1≠0,
∴{an+1}是等比数列.…(4分)
(2)解:由an+1≥an,a1=1,得an≥1,
∴
2
| ||
| an+1 |
∴m≥-an2-2an,…(6分)
∴m≥-(an+1)2+1恒成立,
∵an≥1,∴m≥-22+1=-3,
∴当m≥-3时,能使数列{an}满足不等式an+1≥an恒成立.…(9分)
(3)证明:由(2)得当-3≤m<1时,an+1≥an,∴an>0,
设cn=
| 1 |
| an+1 |
则cn+1=
| 1 |
| an+1+1 |
| 1 | ||
|
| an+1 |
| 2(an+1)2+m-1 |
∵m<1,∴m-1<0,
∴cn+1>
| an+1 |
| 2(an+1)2 |
| 1 |
| 2(an+1) |
| 1 |
| 2 |
∵c1=
| 1 |
| a1+1 |
| 1 |
| 2 |
∴cn>
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
∴c1+c2+c3+…cn>
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| ||||
1-
|
| 1 |
| 2n |
∴
| 1 |
| a1+1 |
| 1 |
| a2+1 |
| 1 |
| an+1 |
| 1 |
| 2n |
点评:本题考查数列为等比数列的证明,考查使不等式恒成立的实数的取值范围的求法,考查不等式的证明,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
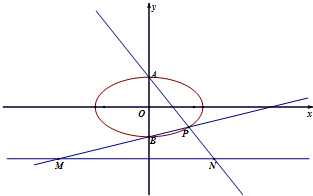 已知椭圆C:
已知椭圆C: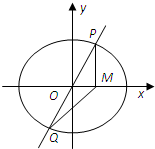 已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为
已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为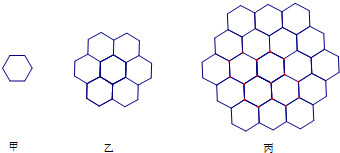 如图,一组蜂巢的截面图,其中第一个图甲有一个蜂巢,第二个图乙有7个蜂巢,第三个图丙有19个蜂巢,按此规律,以f(n)表示第n个图蜂巢总数,则f(4)=
如图,一组蜂巢的截面图,其中第一个图甲有一个蜂巢,第二个图乙有7个蜂巢,第三个图丙有19个蜂巢,按此规律,以f(n)表示第n个图蜂巢总数,则f(4)=