题目内容
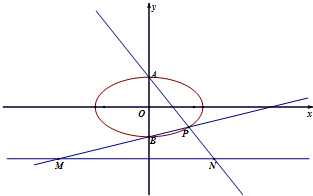 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程.
(2)设A、B是椭圆C的上、下顶点,P是椭圆上异于A、B的任意一点,记直线PA的斜率为k,PB的斜率为m,求证:mk是定值.
(3)在(2)的条件下,直线PA、直线PB分别交直线y=-2于点N、M,P到Y=-2的距离为d,求
| |MN| |
| d |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推出
,由此能求出椭圆C的方程.
(2)由已知条件得A(0,1),B(0,-1),设P(x0,y0),则y02-1=-
,由k =
,m=
,能求出mk是定值-
.
(3)直线PA:y=kx+1,交直线y=-2于N(-
,0),直线PB:y=mx-1,交直线y=-2于M(-
,0),P到y=-2的距离d=
,由此能求出
的最小值.
|
(2)由已知条件得A(0,1),B(0,-1),设P(x0,y0),则y02-1=-
| x02 |
| 4 |
| y0-1 |
| x0 |
| y0+1 |
| x0 |
| 1 |
| 4 |
(3)直线PA:y=kx+1,交直线y=-2于N(-
| 3 |
| k |
| 1 |
| m |
| y0+2 | ||
|
| |MN| |
| d |
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)的离心率为
,a+b=3,
∴
,解得a=2,b=1,
∴椭圆C的方程为
+y2=1.
(2)证明:∵A、B是椭圆C
+y2=1的上、下顶点,
∴A(0,1),B(0,-1),
设P(x0,y0),则
+y02=1,∴y02-1=-
,
由k =
,m=
,
得km=
•
=
=
=-
,
∴mk是定值-
.
(3)解:直线PA:y=kx+1,交直线y=-2于N(-
,0),
直线PB:y=mx-1,交直线y=-2于M(-
,0),
∴|MN|=-
+
=
=4(3m-k)
=4[
-
]=
.
P到y=-2的距离d=
=
,
∴
=
=
≥
=4
.
∴
的最小值为4
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
|
∴椭圆C的方程为
| x2 |
| 4 |
(2)证明:∵A、B是椭圆C
| x2 |
| 4 |
∴A(0,1),B(0,-1),
设P(x0,y0),则
| x02 |
| 4 |
| x02 |
| 4 |
由k =
| y0-1 |
| x0 |
| y0+1 |
| x0 |
得km=
| y0-1 |
| x0 |
| y0+1 |
| x0 |
| y02-1 |
| x02 |
-
| ||
| x02 |
| 1 |
| 4 |
∴mk是定值-
| 1 |
| 4 |
(3)解:直线PA:y=kx+1,交直线y=-2于N(-
| 3 |
| k |
直线PB:y=mx-1,交直线y=-2于M(-
| 1 |
| m |
∴|MN|=-
| 3 |
| k |
| 1 |
| m |
| k-3m |
| mk |
=4[
| 3(y0+1) |
| x0 |
| y0-1 |
| x0 |
| 8(y0+2) |
| x0 |
P到y=-2的距离d=
| |y0+2| | ||
|
| y0+2 | ||
|
∴
| |MN| |
| d |
| ||||
|
8
| ||
| x0 |
8
| ||
| 2 |
| 2 |
∴
| |MN| |
| d |
| 2 |
点评:本题考查椭圆方程的求法,考查两直线的乘积是定值的证明,考查两线段比值为紧小值的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
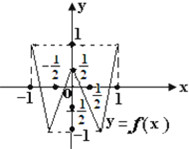 已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是( )
已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是( )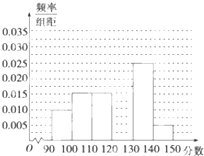 某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: