题目内容
(1)已知
+
=4,其中x>0,y>0,求xy的最小值,及此时x与y的值.
(2)关于x的不等式(x+1)(x-a)≤0,讨论x的解.
| 2 |
| x |
| 1 |
| y |
(2)关于x的不等式(x+1)(x-a)≤0,讨论x的解.
考点:基本不等式
专题:不等式的解法及应用
分析:(1)根据基本不等式,化简计算即可,
(2)根据分类讨论的思想,分a于-1的关系,然后解不等式即可.
(2)根据分类讨论的思想,分a于-1的关系,然后解不等式即可.
解答:
解:(1)x>0,y>0,
+
=4≥2
,化简得xy≥
,所以xy的最小值为
当且仅当
=
时取等号,
∵
+
=4,
∴x=1,y=
(2)当a=-1时,x=-1;
当a>-1时,-1≤x≤a;
当a<-1时,a≤x≤-1.
| 2 |
| x |
| 1 |
| y |
|
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当
| x |
| 2 |
| 1 |
| y |
∵
| 2 |
| x |
| 1 |
| y |
∴x=1,y=
| 1 |
| 2 |
(2)当a=-1时,x=-1;
当a>-1时,-1≤x≤a;
当a<-1时,a≤x≤-1.
点评:本题主要考查了基本不等式的应用和不等式解集的求法,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
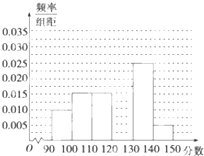 某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某学校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: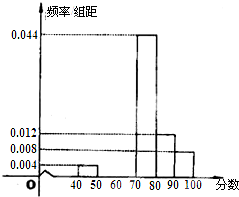 南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员. 某种产品特约经销商根据以往当地的需求情况,得出如图该种产品日需求量的频率分布直方图.
某种产品特约经销商根据以往当地的需求情况,得出如图该种产品日需求量的频率分布直方图.