题目内容
已知数列{an}满足前n项和Sn=2n+1-2．
（1）求数列{an}的通项公式；
（2）设数列{bn}满足bn=（2n+1）•an，求数列{bn}的前n项和Tn．
（1）求数列{an}的通项公式；
（2）设数列{bn}满足bn=（2n+1）•an，求数列{bn}的前n项和Tn．
考点：数列的求和
专题：等差数列与等比数列
分析：（1）根据an与Sn的关系，即可求数列{an}的通项公式；
（2）求出bn=（2n+1）•an的通项公式，利用错位相减法，即可求数列{bn}的前n项和Tn．
（2）求出bn=（2n+1）•an的通项公式，利用错位相减法，即可求数列{bn}的前n项和Tn．
解答：
解：（1）当n≥2时，an=Sn-Sn-1=2n+1-2-（2n-2）=2n+1-2n=2n，
当n=1时，a1=S1=21+1-2=4-2=2，满足an=2n，
∴an=2n，
即数列{an}为等比数列，
∴an=2n．
（2）∵bn=（2n+1）•an，
∴bn=（2n+1）•2n，
则数列{bn}的前n项和Tn=3×2+5×22+7×23+…+（2n+1）•2n，
2Tn=3×22+5×23+7×24+…+（2n-1）•2n+（2n+1）•2n+1，
两式相减得-Tn=6+2×22+2×23+2×24+…+2•2n-（2n+1）•2n+1=6+2×
-（2n+1）•2n+1=-2-（2n-1）2n+1，
即Tn=2+（2n-1）2n+1
当n=1时，a1=S1=21+1-2=4-2=2，满足an=2n，
∴an=2n，
即数列{an}为等比数列，
∴an=2n．
（2）∵bn=（2n+1）•an，
∴bn=（2n+1）•2n，
则数列{bn}的前n项和Tn=3×2+5×22+7×23+…+（2n+1）•2n，
2Tn=3×22+5×23+7×24+…+（2n-1）•2n+（2n+1）•2n+1，
两式相减得-Tn=6+2×22+2×23+2×24+…+2•2n-（2n+1）•2n+1=6+2×
| 4(1-2n-1) |
| 1-2 |
即Tn=2+（2n-1）2n+1
点评：本题主要考查数列通项公式的求解和数列求和，要求熟练掌握错位相减法．考查学生的计算能力．
练习册系列答案
相关题目
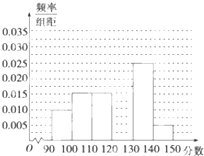某学校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[90，100），[100，110），…，[140，150）后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：
某种产品特约经销商根据以往当地的需求情况，得出如图该种产品日需求量的频率分布直方图．