题目内容
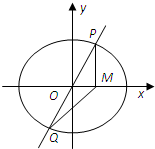 已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为
已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为| 1 |
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)求直线l的方程,使△PQM的面积最大,并求出这个最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设椭圆方程为
+
=1(a>b>0),由已知条件推导出c=1,
=
,由此能求出椭圆C的标准方程.
(Ⅱ)由
,得:3x2+4k2x2=12,由此利用三角形面积公式和均值定理能求出直线l的方程和△PQM的面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| 1 |
| 2 |
(Ⅱ)由
|
解答:
解:(Ⅰ)设椭圆方程为
+
=1(a>b>0),
∵椭圆C的两焦点F1(-1,0)、F2(1,0),
∴c=1…(1分)
∵椭圆C的离心率为
,∴
=
,
解得a=2,b2=3…(3分)
∴椭圆C的标准方程为:
+
=1. …(4分)
(Ⅱ)由
,得:3x2+4k2x2=12,
xP2=
…(6分)
S△PQM=2S△OPM=2×
|OM|•|PM|=|xP|•|yp|=kxP2
=
…(8分)
=
≤
=
…(10分)
当且仅当4k=
,即k=
时取等号,…(11分)
此时,直线l的方程为:y=
x,
△PQM的面积的最大值为
.…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆C的两焦点F1(-1,0)、F2(1,0),
∴c=1…(1分)
∵椭圆C的离心率为
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
解得a=2,b2=3…(3分)
∴椭圆C的标准方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)由
|
xP2=
| 12 |
| 4k2+3 |
S△PQM=2S△OPM=2×
| 1 |
| 2 |
=
| 12k |
| 4k2+3 |
=
| 12 | ||
4k+
|
| 12 | ||
2
|
| 3 |
当且仅当4k=
| 3 |
| k |
| ||
| 2 |
此时,直线l的方程为:y=
| ||
| 2 |
△PQM的面积的最大值为
| 3 |
点评:本题主要考查直线与椭圆的有关知识、函数求最值的方法,数形结合的思想方法和运算求解能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
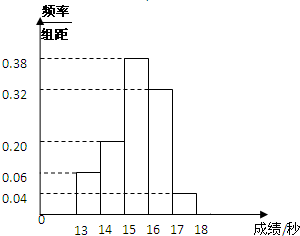 某班50名学生在一次百米测试中,成绩(单位:秒)全部介于13与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩,求这两个成绩一个在第一组,一个在第五组的概率.
某班50名学生在一次百米测试中,成绩(单位:秒)全部介于13与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩,求这两个成绩一个在第一组,一个在第五组的概率.