题目内容
14.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$经过一、三象限的渐近线为m,若圆${x^2}+{y^2}-2\sqrt{5}x-2\sqrt{5}y+6=0$上至少有三个不同的点到m的距离为1,则此双曲线的离心率e的取值范围为( )| A. | $[{\frac{{\sqrt{5}}}{2},2\sqrt{5}}]$ | B. | $({1,\sqrt{5}}]$ | C. | $[{\frac{{\sqrt{5}}}{2},\sqrt{5}}]$ | D. | $[{\sqrt{5},2\sqrt{5}}]$ |
分析 圆${x^2}+{y^2}-2\sqrt{5}x-2\sqrt{5}y+6=0$上至少有三个不同的点到m的距离为1,可得圆心到直线的距离小于等于1,建立不等式,即可求出双曲线的离心率e的取值范围.
解答 解:圆${x^2}+{y^2}-2\sqrt{5}x-2\sqrt{5}y+6=0$,可化为(x-$\sqrt{5}$)2+(y-$\sqrt{5}$)2=4,
∵圆${x^2}+{y^2}-2\sqrt{5}x-2\sqrt{5}y+6=0$上至少有三个不同的点到m的距离为1,
∴圆心到直线的距离小于等于1,
∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$经过一、三象限的渐近线为m:bx-ay=0,
∴$\frac{|\sqrt{5}b-\sqrt{5}a|}{\sqrt{{b}^{2}+{a}^{2}}}$≤1,
∴2b2-5ab+2a2≤0,
∴$\frac{1}{2}$≤$\frac{b}{a}$≤2,
∴1+$\frac{1}{4}$≤1+($\frac{b}{a}$)2≤5,
∴$\frac{\sqrt{5}}{2}$≤e≤$\sqrt{5}$.
点评 本题考查双曲线的离心率e的取值范围,考查直线与圆的位置关系,考查点到直线的距离公式,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1.已知空间非零向量$\overrightarrow{{s}_{1}}$,$\overrightarrow{{s}_{2}}$,则“cos<$\overrightarrow{{s}_{1}}$,$\overrightarrow{{s}_{2}}$>=$\frac{1}{2}$”是“$\overrightarrow{{s}_{1}}$与$\overrightarrow{{s}_{2}}$的夹角为$\frac{π}{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.将函数y=f(x)cosx的图象向左平移$\frac{π}{4}$个单位后,得到函数y=2cos2x-1的图象,则f(x)=( )
| A. | 2sinx | B. | 2cosx | C. | -2sinx | D. | -2cosx |
2.函数y=$lo{g}_{\frac{1}{2}}sin(2πx+\frac{π}{4})$的单调递减区间是( )
| A. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | B. | (-$\frac{1}{8}$+k,$\frac{1}{8}$+k](k∈Z) | C. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | D. | [$\frac{1}{8}$+k,$\frac{3}{8}$+k)(k∈Z) |
9.某几何体的三视图如图所示,则此几何体的体积等于( )
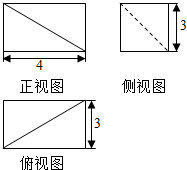

| A. | 45 | B. | 36 | C. | 30 | D. | 6 |
3.执行如图所示的程序框图,若输入的c的值为3,则输出的结果是( )


| A. | 27 | B. | 9 | C. | 8 | D. | 3 |