题目内容

3．某几何体的三视图如图所示，其中俯视图是正方形，那么该几何体的表面积是（　　）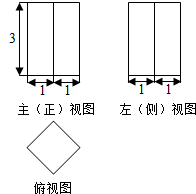
A．32B．24C．$4+12\sqrt{2}$D．$12\sqrt{2}$

分析 由几何体的三视图得出原几何体一个底面为正方形的长方体，结合图中数据求出它的表面积．

解答 解：由三视图可知，该几何体是一个底面为正方形的长方体，
长方体的底面正方形的对角线长为2，长方体的高是3；
所以，底面正方形的边长为$\sqrt{{1}^{2}{+1}^{2}}$=$\sqrt{2}$，
该长方体的表面积为2×${（\sqrt{2}）}^{2}$+4×3×$\sqrt{2}$=4+12$\sqrt{2}$．
故选：C．

点评 本题考查了由几何体的三视图求表面积的应用问题，也考查了空间想象能力和逻辑思维能力，是基础题．

练习册系列答案
相关题目
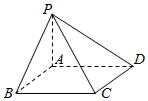13．如图，四棱锥P-ABCD的底面是边长为4的正方形ABCD，侧棱PA垂直于底面，且PA=3．
（1）求异面直线PB与CD所成的角的大小；（结果用反三角函数表示）
（2）求四棱锥P-ABCD的体积．
14．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$e=\frac{{\sqrt{2}}}{2}$，并且椭圆经过点$（-1，\frac{{\sqrt{2}}}{2}）$，F为椭圆的左焦点．
（1）求椭圆的方程
（2）设过点F的直线交椭圆于A，B两点，并且线段AB的中点在直线x+y=0上，求直线AB的直线方程．
11．已知点P（x0，3）与点Q（x0，4）分别在椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1与抛物线y2=2px（p＞0）上．
（1）求抛物线的方程；
（2）设点A（x1，y1），B（x2，y2）（y1≤0，y2≤0）是抛物线上的两点，∠AQB的角平分线与x轴垂直，求直线AB在y轴上的截距的取值范围．
18．已知函数f（x）=x3-ax2-3x．
（1）若f（x）在[1，+∞）上是增函数，求实数a的取值范围；
（2）已知函数g（x）=1n（1+x）-x+$\frac{k}{2}$x2（k≥0），讨论函数g（x）的单调性．
8．已知函数f（x）=ln（x+1）-kx2+k（k∈R）．
（1）若函数f（x）过P（0，1），求f（x）在点P处的切线方程；
（2）求函数f（x）的单调区间．
15．（1）证明：函数y=xsinx+cosx在区间（$\frac{3}{2}$π，$\frac{5}{2}$π）内是增函数．
（2）证明：函数f（x）=ex+e-x在[0，+∞）上是增函数．
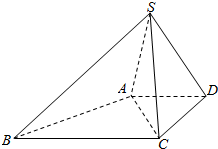12．如图，在底面为梯形的四棱锥S-ABCD中，已知AD∥BC，∠ASC=60°，AD=DC=$\sqrt{2}$，SA=SC=SD=2．
（Ⅰ）求证：AC⊥SD；
（Ⅱ）求三棱锥B-SAD的体积．
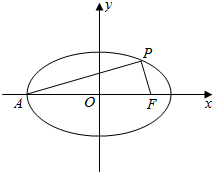13．如图，在平面直角坐标系xOy中，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点为A，右焦点为F（c，0），P（x0，y0）为椭圆上一点且PA⊥PF．
（1）若a=3，b=$\sqrt{5}$，求△AFP的面积；
（2）求证：以F为圆心，FP为半径的圆与直线x=$\frac{{a}^{2}}{c}$相切．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网