题目内容
11.已知点P(x0,3)与点Q(x0,4)分别在椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1与抛物线y2=2px(p>0)上.(1)求抛物线的方程;
(2)设点A(x1,y1),B(x2,y2)(y1≤0,y2≤0)是抛物线上的两点,∠AQB的角平分线与x轴垂直,求直线AB在y轴上的截距的取值范围.
分析 (1)分别代入P,Q的坐标,解方程求得P即可点到抛物线的方程;
(2)根据条件判定直线QA、QB的斜率关系,求出直线AB的斜率,再设出直线AB的方程,和抛物线方程联立后化为关于y的一元二次方程,由判别式大于0,且y1y2≥0,求得直线AB在y轴上的截距的取值范围.
解答 解:(1)由题意可得$\frac{{{x}_{0}}^{2}}{16}$+$\frac{9}{12}$=1,
解得x0=2(-2舍去),
即有点Q(2,4)分别在抛物线y2=2px上,
即有16=4p,
解得p=4,则有抛物线的方程为y2=8x;
(2)由(1)知点Q的坐标为(2,4),
由∠AQB的角平分线与x轴垂直,
可得QA、QB的倾斜角互补,即QA、QB的斜率互为相反数,
设QA的斜率为k,则QA:y-4=k(x-2),k≠0,
与抛物线方程联立,可得y2-$\frac{8}{k}$y-16+$\frac{32}{k}$=0,
方程的解为4、y1,
由韦达定理得:y1+4=$\frac{8}{k}$,即y1=$\frac{8}{k}$-4,
同理y2=-$\frac{8}{k}$-4,
又y12=8x1,y22=8x2,
∴kAB=-1,
设AB:y=-x+b,与抛物线方程联立可得y2+8y-8b=0,
由韦达定理得:y1+y2=-8,y1y2=-8b,
∵△=64+32b>0⇒b>-2,y1•y2=-8b≥0⇒b≤0,
∴-2<b≤0,
即直线AB在y轴上的截距的取值范围是(-2,0].
点评 本题考查抛物线方程的求法,考查直线和圆锥曲线的位置关系,训练了一元二次方程有两不等根的条件的应用,是中档题.

练习册系列答案
相关题目
1.已知实数20、m2、52构成一个等差数列,则圆锥曲线$\frac{{x}^{2}}{m}+{y}^{2}=1$的离心率为( )
| A. | $\frac{\sqrt{30}}{6}$ | B. | $\sqrt{7}$ | C. | $\frac{\sqrt{30}}{6}$或$\sqrt{7}$ | D. | $\frac{5}{6}$或7 |
3.某几何体的三视图如图所示,其中俯视图是正方形,那么该几何体的表面积是( )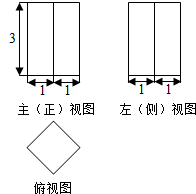

| A. | 32 | B. | 24 | C. | $4+12\sqrt{2}$ | D. | $12\sqrt{2}$ |
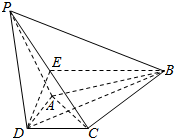 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.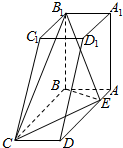 如图所示的几何体A1B1C1D1-ABCD中,平面A1B1C1D1∥平面ABCD,A1B1C1D1是边长为2的正方形,ABCD是矩形,AD=5,AA1B1B是矩形,A1A⊥平面ABCD,E为AD上的一点,AE=1.
如图所示的几何体A1B1C1D1-ABCD中,平面A1B1C1D1∥平面ABCD,A1B1C1D1是边长为2的正方形,ABCD是矩形,AD=5,AA1B1B是矩形,A1A⊥平面ABCD,E为AD上的一点,AE=1.