题目内容
14.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{2}}}{2}$,并且椭圆经过点$(-1,\frac{{\sqrt{2}}}{2})$,F为椭圆的左焦点.(1)求椭圆的方程
(2)设过点F的直线交椭圆于A,B两点,并且线段AB的中点在直线x+y=0上,求直线AB的直线方程.
分析 (1)运用离心率公式和a,b,c的关系,代入点的坐标,解方程可得a,b,进而得到椭圆的方程;
(2)设直线AB的方程为y=k(x+1),代入椭圆方程,运用韦达定理和中点坐标公式,求得中点的坐标,代入直线x+y=0,解方程可得k,进而得到所求直线方程.
解答 解:(1)e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2-b2=c2,
即有a=$\sqrt{2}$c=$\sqrt{2}$b,
又$\frac{1}{{a}^{2}}$+$\frac{1}{2{b}^{2}}$=1,解得a=$\sqrt{2}$,b=1,
即有椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)F(-1,0),设直线AB的方程为y=k(x+1),
代入椭圆方程可得,(1+2k2)x2+4k2x+2k2-2=0,
即有x1+x2=-$\frac{4{k}^{2}}{1+2{k}^{2}}$,
则AB的中点坐标为(-$\frac{2{k}^{2}}{1+2{k}^{2}}$,$\frac{k}{1+2{k}^{2}}$),
由AB的中点在直线x+y=0上,可得-$\frac{2{k}^{2}}{1+2{k}^{2}}$+$\frac{k}{1+2{k}^{2}}$=0,
解得k=$\frac{1}{2}$或0,
则所求直线AB的方程为y=0或y=$\frac{1}{2}$x+$\frac{1}{2}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和点满足椭圆方程,考查直线方程的求法,注意运用直线方程代入椭圆方程,运用中点坐标公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
17.若x是三角形的最小内角,则函数y=sinx+cosx-sinxcosx的最小值是( )
| A. | -$\frac{1}{2}$+$\sqrt{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | 1 | D. | $\sqrt{2}$ |
5.如图为一个几何体的三视图,则该几何体的体积为( )
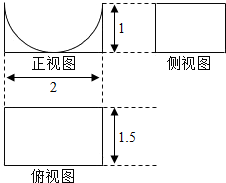

| A. | 6-$\frac{3π}{4}$ | B. | 6-$\frac{3π}{2}$ | C. | 3-$\frac{3π}{2}$ | D. | 3-$\frac{3π}{4}$ |
3.某几何体的三视图如图所示,其中俯视图是正方形,那么该几何体的表面积是( )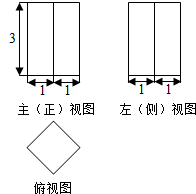

| A. | 32 | B. | 24 | C. | $4+12\sqrt{2}$ | D. | $12\sqrt{2}$ |
4.某几何体的三视图如图,则该几何体的表面积为( )
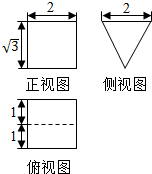

| A. | $12+\sqrt{3}$ | B. | $12+2\sqrt{3}$ | C. | $4+3\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
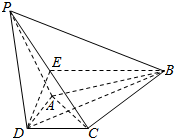 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.