题目内容
13.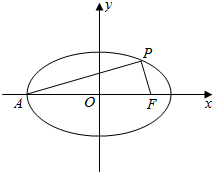 如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,右焦点为F(c,0),P(x0,y0)为椭圆上一点且PA⊥PF.
如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,右焦点为F(c,0),P(x0,y0)为椭圆上一点且PA⊥PF.(1)若a=3,b=$\sqrt{5}$,求△AFP的面积;
(2)求证:以F为圆心,FP为半径的圆与直线x=$\frac{{a}^{2}}{c}$相切.
分析 (1)a=3,b=$\sqrt{5}$,可得c=$\sqrt{{a}^{2}-{b}^{2}}$.可得椭圆的标准方程为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1.于是$\frac{{x}_{0}^{2}}{9}$+$\frac{{y}_{0}^{2}}{5}$=1,由于PA⊥PF,可得$\overrightarrow{PA}•\overrightarrow{PF}$=0,化为:(x0+3)(x0-2)+${y}_{0}^{2}$=0,联立解出,利用△AFP的面积S=$\frac{1}{2}{y}_{0}$(a+c)即可得出.
(2)依题意,椭圆右焦点到直线x=
| a2 |
| c |
| a2 |
| c |
| x02 |
| a2 |
| y02 |
| b2 |
| a(a2-ac-c2) |
| c2 |
| (x0-c)2+y02 |
解答 (1)解:∵a=3,b=$\sqrt{5}$,∴c=$\sqrt{{a}^{2}-{b}^{2}}$=2.
∴椭圆的标准方程为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1.
∴$\frac{{x}_{0}^{2}}{9}$+$\frac{{y}_{0}^{2}}{5}$=1,
∵PA⊥PF,
∴$\overrightarrow{PA}•\overrightarrow{PF}$=0,
化为:(x0+3)(x0-2)+${y}_{0}^{2}$=0,
联立解得:y0=$\frac{5\sqrt{3}}{4}$.
∴△AFP的面积S=$\frac{1}{2}{y}_{0}$(a+c)=$\frac{1}{2}×\frac{5\sqrt{3}}{4}$×5=$\frac{25\sqrt{3}}{8}$.(2)
(2)证明:依题意,椭圆右焦点到直线x=
| a2 |
| c |
| a2 |
| c |
| x02 |
| a2 |
| y02 |
| b2 |
由PA⊥PF得,
| y0 |
| x0+a |
| yo |
| x0-c |
由①②得,(x0+a)[x0+
| a(b2-ac) |
| c2 |
解得x0=-
| a(a2-ac-c2) |
| c2 |
所以PF=
| (x0-c)2+y02 |
| (x0-c)2-x02+(c-a)x0+ca |
| c |
| a |
=a+
| c |
| a |
| a(a2-ac-c2) |
| c2 |
| a2 |
| c |
所以以F为圆心,FP为半径的圆与右准线x=
| a2 |
| c |
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、向量垂直与数量积的关系、勾股定理、两点之间的距离公式、直线与圆相切的性质,考查了推理能力与计算能力,属于中档题.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案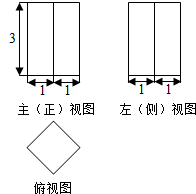
| A. | 32 | B. | 24 | C. | $4+12\sqrt{2}$ | D. | $12\sqrt{2}$ |
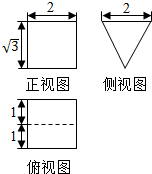
| A. | $12+\sqrt{3}$ | B. | $12+2\sqrt{3}$ | C. | $4+3\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
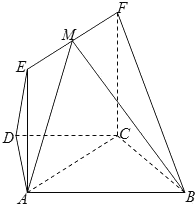 如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.
如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.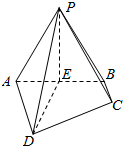 如图,在四棱锥P-ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点
如图,在四棱锥P-ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点