题目内容
8.已知函数f(x)=ln(x+1)-kx2+k(k∈R).(1)若函数f(x)过P(0,1),求f(x)在点P处的切线方程;
(2)求函数f(x)的单调区间.
分析 (1)将P(0,1)代入f(x)求出k=1,从而求出f′(0)即切线的斜率,从而求出切线方程;
(2)求出函数的导数,通过讨论k的范围结合二次函数的性质从而求出函数的单调区间.
解答 解:(1)将P(0,1)代入f(x)得:
f(0)=0-0+k=1,解得:k=1,
∴f(x)=ln(x+1)-x2+1,
∴f′(x)=$\frac{1}{x+1}$-2x,
f′(0)=1,
故过P(0,1),斜率是1的直线为:y-1=x,
即x-y+1=0;
(2)f(x)的定义域是(-1,+∞),
f′(x)=$\frac{-2{kx}^{2}-2kx+1}{x+1}$,
令g(x)=-2kx2-2kx+1,
①k=0时,g(x)=1>0,即f′(x)>0,
∴f(x)在定义域(-1,+∞)递增,
②k>0时,-2k<0,
△=4k2+8k>0,
x1=k-$\sqrt{{k}^{2}+2k}$>-1,x2=k+$\sqrt{{k}^{2}+2k}$,
∴f(x)在(-1,k-$\sqrt{{k}^{2}+2k}$)递减,在(k-$\sqrt{{k}^{2}+2k}$,k+$\sqrt{{k}^{2}+2k}$)递增,在(k+$\sqrt{{k}^{2}+2k}$,+∞)递减;
②k<0时,-2k>0,
△=4k2+8k,
令△>0,解得:k<-2,
∴-2≤k<0时,g(x)≥0,
f(x)在定义域(-1,+∞)递增,
k<-2时,
x1=k-$\sqrt{{k}^{2}+2k}$<-2,x2=k+$\sqrt{{k}^{2}+2k}$<-1,都舍去,
∴f(x)在(-1,+∞)递增;
综上,k≤0时,f(x)在定义域递增,
k>0时,f(x)在(-1,k-$\sqrt{{k}^{2}+2k}$)递减,在(k-$\sqrt{{k}^{2}+2k}$,k+$\sqrt{{k}^{2}+2k}$)递增,在(k+$\sqrt{{k}^{2}+2k}$,+∞)递减.
点评 本题考察了求曲线的切线方程问题,考察导数的应用,二次函数的性质,是一道中档题.

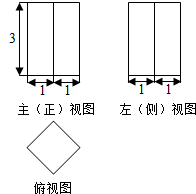
| A. | 32 | B. | 24 | C. | $4+12\sqrt{2}$ | D. | $12\sqrt{2}$ |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
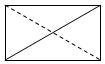
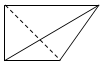
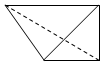
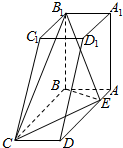 如图所示的几何体A1B1C1D1-ABCD中,平面A1B1C1D1∥平面ABCD,A1B1C1D1是边长为2的正方形,ABCD是矩形,AD=5,AA1B1B是矩形,A1A⊥平面ABCD,E为AD上的一点,AE=1.
如图所示的几何体A1B1C1D1-ABCD中,平面A1B1C1D1∥平面ABCD,A1B1C1D1是边长为2的正方形,ABCD是矩形,AD=5,AA1B1B是矩形,A1A⊥平面ABCD,E为AD上的一点,AE=1.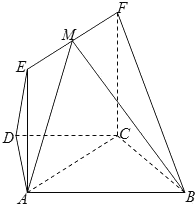 如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.
如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.