题目内容
15.(1)证明:函数y=xsinx+cosx在区间($\frac{3}{2}$π,$\frac{5}{2}$π)内是增函数.(2)证明:函数f(x)=ex+e-x在[0,+∞)上是增函数.
分析 求出函数的导数,判断函数的导数在区间上的符号,利用导函数的符号,判断函数的单调性即可证明本题.
解答 证明:(1)函数y=xsinx+cosx,
则函数y′=sinx+xcosx-sinx=xcosx.
∵x∈($\frac{3}{2}$π,$\frac{5}{2}$π),
∴cosx>0,
∴xcosx>0,即x∈($\frac{3}{2}$π,$\frac{5}{2}$π),y′>0恒成立,
∴函数y=xsinx+cosx在区间(,)上是增函数;
(2):∵f(x)=ex+e-x
∴f′(x)=ex-e-x
令f′(x)≥0得,x≥0,
函数f(x)=ex+e-x在[0,+∞)上是增函数.
点评 本题考查函数的导数的应用,函数的单调性的判断,考查分析问题解决问题的能力.

练习册系列答案
相关题目
5.如图为一个几何体的三视图,则该几何体的体积为( )
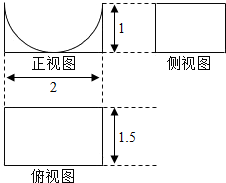

| A. | 6-$\frac{3π}{4}$ | B. | 6-$\frac{3π}{2}$ | C. | 3-$\frac{3π}{2}$ | D. | 3-$\frac{3π}{4}$ |
3.某几何体的三视图如图所示,其中俯视图是正方形,那么该几何体的表面积是( )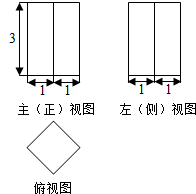

| A. | 32 | B. | 24 | C. | $4+12\sqrt{2}$ | D. | $12\sqrt{2}$ |
10.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,点P满足|PF1|+|PF2|>2a,则( )
| A. | 点P在椭圆C外 | B. | 点P在椭圆C内 | ||
| C. | 点P在椭圆C上 | D. | 点P与椭圆C的位置关系不能确定 |
4.某几何体的三视图如图,则该几何体的表面积为( )
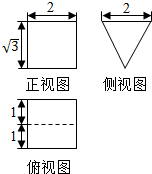

| A. | $12+\sqrt{3}$ | B. | $12+2\sqrt{3}$ | C. | $4+3\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
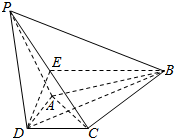 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.