题目内容
13.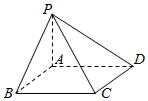 如图,四棱锥P-ABCD的底面是边长为4的正方形ABCD,侧棱PA垂直于底面,且PA=3.
如图,四棱锥P-ABCD的底面是边长为4的正方形ABCD,侧棱PA垂直于底面,且PA=3.(1)求异面直线PB与CD所成的角的大小;(结果用反三角函数表示)
(2)求四棱锥P-ABCD的体积.
分析 (1)由AB∥CD可知∠PBA是异面直线PB与CD所成的角,且PA⊥AB,得出tan∠PBA=$\frac{PA}{AB}$=$\frac{3}{4}$.
(2)由PA⊥底面ABCD可知PA为棱锥的高,代入体积公式即可求出棱锥的体积.
解答 解:(1)∵四边形ABCD是正方形,∴AB∥CD,AB=CD,
∴∠PBA是异面直线PB与CD所成的角,
∵PA⊥底面ABCD,AB?平面ABCD,
∴PA⊥AB,
∴tan∠PBA=$\frac{PA}{AB}$=$\frac{3}{4}$.∴∠PBA=arctan$\frac{3}{4}$.
(2)V棱锥P-ABCD=$\frac{1}{3}$S正方形ABCD•PA=$\frac{1}{3}×{4}^{2}×3$=16.
点评 本题考查了空间角的计算,空间几何体的体积计算,正确作出空间角是解题关键.

练习册系列答案
相关题目
17.若x是三角形的最小内角,则函数y=sinx+cosx-sinxcosx的最小值是( )
| A. | -$\frac{1}{2}$+$\sqrt{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | 1 | D. | $\sqrt{2}$ |
1.已知实数20、m2、52构成一个等差数列,则圆锥曲线$\frac{{x}^{2}}{m}+{y}^{2}=1$的离心率为( )
| A. | $\frac{\sqrt{30}}{6}$ | B. | $\sqrt{7}$ | C. | $\frac{\sqrt{30}}{6}$或$\sqrt{7}$ | D. | $\frac{5}{6}$或7 |
5.如图为一个几何体的三视图,则该几何体的体积为( )
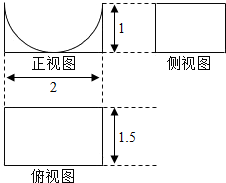

| A. | 6-$\frac{3π}{4}$ | B. | 6-$\frac{3π}{2}$ | C. | 3-$\frac{3π}{2}$ | D. | 3-$\frac{3π}{4}$ |
3.某几何体的三视图如图所示,其中俯视图是正方形,那么该几何体的表面积是( )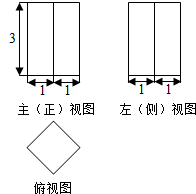

| A. | 32 | B. | 24 | C. | $4+12\sqrt{2}$ | D. | $12\sqrt{2}$ |