题目内容
12.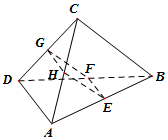 (文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,
(文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,(1)求证:四边形EFGH是平行四边形.
(2)求证:BC∥平面EFGH.
分析 (1)推导出EF$\underset{∥}{=}$$\frac{1}{2}AD$,GH$\underset{∥}{=}$$\frac{1}{2}AD$,从而EF$\underset{∥}{=}$GH,由此能证明四边形EFGH是平行四边形.
(2)推导出EH∥BC,由此能证明BC∥平面EFGH.
解答 证明:(1)∵在空间四面体ABCD中,
E,F,G,H分别是AB,BD,CD,AC的中点,
∴EF$\underset{∥}{=}$$\frac{1}{2}AD$,GH$\underset{∥}{=}$$\frac{1}{2}AD$,
∴EF$\underset{∥}{=}$GH,
∴四边形EFGH是平行四边形.
(2)∵E,H分别是AB、AC的中点,
∴EH∥BC,
∵EH?平面EFGH,BC?平面EFGH,
∴BC∥平面EFGH.
点评 本题考查四边形是平行四边形的证明,考查线面平行的证明,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1533石,验得米内夹谷,抽样取米一把,数得254粒内夹谷56粒,则这批米内夹谷约为( )
| A. | 1365石 | B. | 338石 | C. | 168石 | D. | 134石 |
20.若x,y是正数,且$\frac{1}{x}+\frac{4}{y}=1$,则x+y有( )
| A. | 最小值9 | B. | 最大值9 | C. | 最小值$5+2\sqrt{2}$ | D. | 最大值$5+2\sqrt{2}$ |
4.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了五次试验,得到的数据如下,由最小二乘法求得回归方程$\hat y=0.67x+54.9$,现发有一个数据看不清,请你推断出该
数据的值为67.
| 零件个数x | 10 | 20 | 30 | 40 | 50 |
| 加工时间y分钟 | 63 | ? | 75 | 82 | 88 |
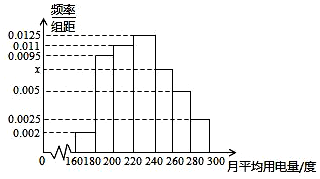 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.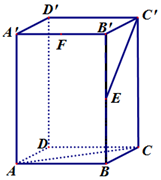 如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.
如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.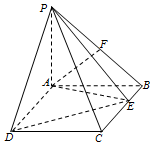 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.