题目内容
15.如图,曲线y=f(x)在点P(5,f(5))处的切线方程是y=-x+8,则f(5)+f'(5)=2.
分析 根据题意,由图象和切线方程可得:f(5)=-5+8=3,f′(5)=-1.即可得到结果.
解答 解:由于曲线f(x)在点P(5,f(5))处的切线方程是y=-x+8,
则f(5)=-5+8=3,f′(5)=-1.
故f(5)+f′(5)=3-1=2.
故答案为:2.
点评 本题考查导数的计算,关键是理解导数的几何意义.

练习册系列答案
相关题目
5.设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,$f(x)={({\frac{1}{2}})^x}-1$.若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则实数a的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | $({1,\root{4}{3}})$ | D. | $({\root{4}{3},2})$ |
6.球的半径扩大为原来的2倍,它的体积扩大为原来的( )倍.
| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
3.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1533石,验得米内夹谷,抽样取米一把,数得254粒内夹谷56粒,则这批米内夹谷约为( )
| A. | 1365石 | B. | 338石 | C. | 168石 | D. | 134石 |
10.若某个扇形的半径为3cm,弧长为πcm,则该扇形的面积为( )
| A. | πcm2 | B. | $\frac{3}{2}π$cm2 | C. | 3πcm2 | D. | 6πcm2 |
20.若x,y是正数,且$\frac{1}{x}+\frac{4}{y}=1$,则x+y有( )
| A. | 最小值9 | B. | 最大值9 | C. | 最小值$5+2\sqrt{2}$ | D. | 最大值$5+2\sqrt{2}$ |
4.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了五次试验,得到的数据如下,由最小二乘法求得回归方程$\hat y=0.67x+54.9$,现发有一个数据看不清,请你推断出该
数据的值为67.
| 零件个数x | 10 | 20 | 30 | 40 | 50 |
| 加工时间y分钟 | 63 | ? | 75 | 82 | 88 |
5.已知a=-2${\;}^{1-lo{g}_{2}3}$,b=1-log23,c=cos$\frac{5π}{6}$,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
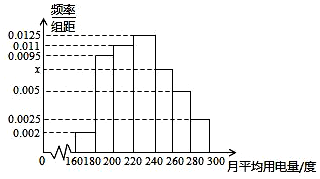 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.