题目内容
已知定义域为R的函数y=f(x)在[0,7]上只有l和3两个零点,且y=f(2-x)与y=f (7+x)都是偶函数,则函数y=f(x)在[0,2013]上的零点个数为( )
| A、402 | B、403 |
| C、404 | D、405 |
考点:函数的周期性,函数奇偶性的性质
专题:函数的性质及应用
分析:根据y=f(2-x)与y=f (7+x)都是偶函数,得到函数f(x)=f(10+x)即函数是周期函数,利用函数的周期性即可得到函数零点的个数.
解答:
解:∵y=f(2-x)与y=f (7+x)都是偶函数,
∴f(2-x)=f(2-x),f (7+x)=f(7-x),
即f(x)关于x=2和x=7对称.
∵f(2-x)=f(2+x),
∴f(4-x)=f(x),
∵f(7-x)=f(7+x),
∴f(4-x)=f(10+x)
∴f(x)=f(10+x),
即10是函数f(x)的一个周期
∵f(7-x)=f(7+x),
函数f(x)在[4,7]上无根.
∴函数f(x)在[7,10]上无根.
∴f(x)=0在[0,10]上恰有两根为1和3,
f(x)=0的根为10n+1或10n+3的形式
∴0≤10n+1≤2013,解得0≤n≤201.2,共202个
∴0≤10n+3≤2013,解得0≤n≤201,共202个
∴方程f(x)=0在闭区间[0,2013]上根的个数为404个.
故选:C.
∴f(2-x)=f(2-x),f (7+x)=f(7-x),
即f(x)关于x=2和x=7对称.
∵f(2-x)=f(2+x),
∴f(4-x)=f(x),
∵f(7-x)=f(7+x),
∴f(4-x)=f(10+x)
∴f(x)=f(10+x),
即10是函数f(x)的一个周期
∵f(7-x)=f(7+x),
函数f(x)在[4,7]上无根.
∴函数f(x)在[7,10]上无根.
∴f(x)=0在[0,10]上恰有两根为1和3,
f(x)=0的根为10n+1或10n+3的形式
∴0≤10n+1≤2013,解得0≤n≤201.2,共202个
∴0≤10n+3≤2013,解得0≤n≤201,共202个
∴方程f(x)=0在闭区间[0,2013]上根的个数为404个.
故选:C.
点评:本题主要考查函数零点的个数的判断,利用函数的奇偶性得到函数的周期性是解决本题的关键,综合考查函数性质的应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
直线l与圆x2+y2+2x-4y+1=0相交于A,B两点,若弦AB的中点(-2,3),则直线l的方程为( )
| A、x+y-3=0 |
| B、x+y-1=0 |
| C、x-y+5=0 |
| D、x-y-5=0 |
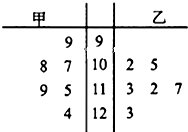 在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示: