题目内容
在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρ=4cosθ,直线l的参数方程是
(t为参数).
(1)设M,N分别为曲线C,直线l上的动点,求|MN|的最小值;
(2)求曲线C上平行于直线l的切线的一般方程.
|
(1)设M,N分别为曲线C,直线l上的动点,求|MN|的最小值;
(2)求曲线C上平行于直线l的切线的一般方程.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(Ⅰ)首先把极坐标方程转化为直角坐标方程的,进一步利用点到直线的距离求解
(Ⅱ)利用斜截式直线方程,利用斜率相等求出结果.
(Ⅱ)利用斜截式直线方程,利用斜率相等求出结果.
解答:
解:(Ⅰ)化极坐标方程为ρ=4cosθ为直角坐标方程x2+y2-4x=0,所以曲线C是以(2,0)为圆心,2为半径的圆.
化参数方程
(t为参数)为普通方程x-
y+3=0则圆心到直线l的距离d=
=
,
所以|MN|的最小值为
-2=
,
(Ⅱ)直线l的斜率为
,设所求切线方程为y=
x+b,即
x-3y+3b=0,则
=2,
所以:b=
或-2
,
所求切线方程为y=
x+
或y=
x-2
,即x-
y+2=0或x-
y-2=0.
化参数方程
|
| 3 |
| |2+3| | ||
|
| 5 |
| 2 |
所以|MN|的最小值为
| 5 |
| 2 |
| 1 |
| 2 |
(Ⅱ)直线l的斜率为
| ||
| 3 |
| ||
| 3 |
| 3 |
|2
| ||
|
所以:b=
2
| ||
| 3 |
| 3 |
所求切线方程为y=
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查的知识要点:极坐标方程和直角坐标方程的互化,点到直线的距离,及斜截式直线方程的应用.

练习册系列答案
相关题目
下列说法中,不正确的是( )
| A、“|x|=|y|”是“x=y”的必要不充分条件 |
| B、命题p:?x∈R,sinx≤1,则¬p:?x∈R,sinx>1 |
| C、“λ≤2”是“数列an=n2-λn+1(n∈N*)为递增数列”的充要条件 |
| D、命题p:所有有理数都是实数,q:正数的对数都是负数,则(¬p)∨(¬q)为真命题 |
如图是一个圆锥的三视图,则其侧面积是( )


| A、π | B、2π | C、3π | D、4π |

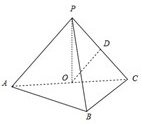 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.