题目内容
已知函数f（x）=3x3-9x+5．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）求函数f（x）在[0，3]上的最大值和最小值．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）求函数f（x）在[0，3]上的最大值和最小值．
考点：利用导数求闭区间上函数的最值
专题：导数的概念及应用
分析：（Ⅰ）先求出函数的导数，解不等式，从而求出函数的单调区间，（Ⅱ）由（Ⅰ）得：f（x）在[0，1）递减，在（1，3]递增，从而求出函数的最值．
解答：
解：（Ⅰ）∵f′（x）=9x2-9，
令f′（x）＞0，解得：x＞1，x＜-1，
令f′（x）＜0，解得：-1＜x＜1，
∴f（x）在（-∞，-1），（1，+∞）递增，在（-1，1）递减；
（Ⅱ）由（Ⅰ）得：
f（x）在[0，1）递减，在（1，3]递增，
∴f（x）最小值=f（1）=-1，f（x）最大值=f（3）=59．
令f′（x）＞0，解得：x＞1，x＜-1，
令f′（x）＜0，解得：-1＜x＜1，
∴f（x）在（-∞，-1），（1，+∞）递增，在（-1，1）递减；
（Ⅱ）由（Ⅰ）得：
f（x）在[0，1）递减，在（1，3]递增，
∴f（x）最小值=f（1）=-1，f（x）最大值=f（3）=59．
点评：本题考查了函数的单调性，函数的最值问题，考查导数的应用，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
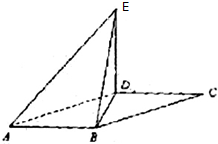如图，平行四边形ABCD中，∠ABD=90°，AB=2，AD=4，将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
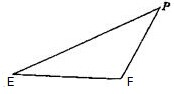在面积为12的△PEF中，已知tan∠PEF=