题目内容
3.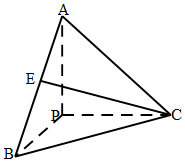 已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.
已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.
分析 建立空间直角坐标系,求出平面PAC的法向量,向量CE,利用空间向量的数量积求解即可.
解答 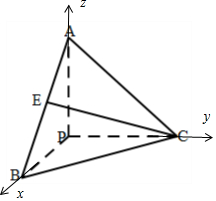 解:PA、PB、PC互相垂直,以P为坐标原点,PA、PB、PC分别为x,y,z轴,
解:PA、PB、PC互相垂直,以P为坐标原点,PA、PB、PC分别为x,y,z轴,
设PA=2,则平面PAC的法向量可以为$\overrightarrow{n}$=(2,0,0),E(1,0,1),C(0,2,0),
$\overrightarrow{CE}$=(1,-2,1),
直线CE与平面PAC所成角的正弦值为:$|\frac{\overrightarrow{n}•\overrightarrow{CE}}{|\overrightarrow{n}||\overrightarrow{CE}|}|$=$\frac{2}{2•\sqrt{6}}$=$\frac{\sqrt{6}}{6}$.
故答案为:$\frac{\sqrt{6}}{6}$.
点评 本题考查直线与平面所成角的求法.考查空间向量数量积的应用,是基础题.

练习册系列答案
相关题目
11.下列函数既是偶函数,又在(0,+∞)上是增函数的是( )
| A. | y=x-2 | B. | $y={x^{\frac{1}{3}}}$ | C. | y=2|x| | D. | y=|x-1|+|x+1| |
15.已知命题p:x2+2x-3>0;命题q:x>a,且¬p是¬q的一个充分不必要条件,则a的取值范围是( )
| A. | (-∞,1] | B. | [1,+∞) | C. | [-1,+∞) | D. | (-∞,-3] |
12.某科研所对新研发的一种产品进行合理定价,该产品按事先拟定的价格试销得统计数据.
(1)①求线性回归方程y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;②谈谈商品定价对市场的影响;
(2)估计在以后的销售中,销量与单价服从回归直线,若该产品的成本为4.5元/件,为使科研所获利最大,该产品定价应为多少?
(附:$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,$\overline{x}$=8.5,$\overline{y}$=80)
| 单价x(万元) | 8 | 8.2 | 8.4 | 8.8 | 8.6 | 9 |
| 销量y(件) | 90 | 84 | 83 | 75 | 80 | 68 |
(2)估计在以后的销售中,销量与单价服从回归直线,若该产品的成本为4.5元/件,为使科研所获利最大,该产品定价应为多少?
(附:$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,$\overline{x}$=8.5,$\overline{y}$=80)
13.若a>0,b>0,且函数f(x)=6x3-ax2-2bx+2在x=1处有极值,若t=ab,则t的最大值为( )
| A. | $\frac{81}{4}$ | B. | 6 | C. | $\frac{81}{2}$ | D. | 9 |
 抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.