题目内容
8.三棱锥A-BCD的底面是正三角形,侧棱相等且两两垂直,点P是该棱锥表面(包括棱)上一点,且P到四个顶点的距离有且只有两个不同的值,则这样的点P的个数有( )| A. | 5 | B. | 6 | C. | 8 | D. | 11 |
分析 由题意符合条件的点有三类,一在棱的中点,二在面的外心,三为四面体的顶点,问题得以解决.
解答 解:如图,
符合条件的点P有三类:(1)6条棱的中点;(2)4个面的外心;③四个顶点.共14个点.
由于三个侧面的外心均与底边中点重合,
∴符合条件的点P有14-3=11.
故选:D.
点评 本题主要考查空间中点、线、面的位置关系,考查空间想象能力和思维能力,关键是理解几何图形,属于中档题.

练习册系列答案
相关题目
18.“B=60°”是“△ABC三个内角A、B、C成等差数列”的( )
| A. | 充分而不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
16.过x轴上一点P作x轴的垂线,分别交函数y=sinx,y=cosx,y=tanx的图象于P1,P2,P3,若$\overrightarrow{P{P_3}}=\frac{3}{8}\overrightarrow{P{P_2}}$,则$|\overrightarrow{P{P_1}}|$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
13.如果函数y=sinωx•cosωx(ω>0)的最小正周期为4π,那么常数ω为( )
| A. | $\frac{1}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | 4 |
17.设α,β是两个不同的平面,a,b是两条不同的直线,下列四个命题中正确的命题是( )
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,b∥β,a∥b,则α∥β | ||
| C. | 若a⊥α,a?β,则α⊥β | D. | 若a,b在α内的射影相互垂直,则a⊥b |
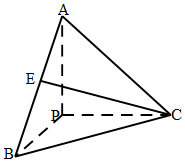 已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.
已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.