题目内容
13.若a>0,b>0,且函数f(x)=6x3-ax2-2bx+2在x=1处有极值,若t=ab,则t的最大值为( )| A. | $\frac{81}{4}$ | B. | 6 | C. | $\frac{81}{2}$ | D. | 9 |
分析 求出导函数,利用函数在极值点处的导数值为0得到a,b满足的条件,利用基本不等式求出ab的最值.
解答 解:由题意,导函数f′(x)=18x2-2ax-2b,
∵在x=1处有极值,
∴a+b=9,
∵a>0,b>0,
∴ab≤($\frac{a+b}{2}$)2=$\frac{81}{4}$,当且仅当a=b=$\frac{9}{2}$时取等号,
∴t=ab的最大值等于$\frac{81}{4}$.
故选:A.
点评 本题考查函数在极值点处的导数值为0、考查利用基本不等式求最值,需注意:一正、二定、三相等.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
4.已知集合A={1,3,5,7,9},B={1,3,9},则∁AB=( )
| A. | {5,7} | B. | {1,3,9} | C. | {3,5,7} | D. | {1,2,3} |
1.方程x-sinx=0的根的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.“a=-2”是“直线(a+2)x+3ay+1=0与直线(a-2)x+(a+2)y-3=0相互垂直”的( )条件.
| A. | 充要 | B. | 充分非必要 | ||
| C. | 必要非充分 | D. | 既非充分也非必要 |
5.命题p:?x0∈R,${x_0}^2-{x_0}+1≤0$,¬p为( )
| A. | ?x∈R,x2-x+1<0 | B. | ?x∈R,x2-x+1>0 | C. | ?x∈R,x2-x+1>0 | D. | ?x∈R,x2-x+1≥0 |
3.甲乙丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,若开始时球在甲手中,则经过三次传球后,球传回甲手中的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
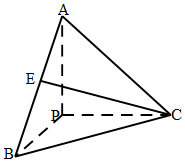 已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.
已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.