题目内容
14.若“m>a”是“函数$f(x)={(\frac{1}{3})^x}+m-\frac{1}{3}$的图象不过第三象限”的必要不充分条件,则实数a能取的最大整数为( )| A. | 1 | B. | 0 | C. | -2 | D. | -1 |
分析 由“函数$f(x)={(\frac{1}{3})^x}+m-\frac{1}{3}$的图象不过第三象限”,可得$m-\frac{1}{3}$≥0,解得m$≥\frac{1}{3}$.即可得出.
解答 解:由“函数$f(x)={(\frac{1}{3})^x}+m-\frac{1}{3}$的图象不过第三象限”,可得$m-\frac{1}{3}$≥0,解得m$≥\frac{1}{3}$.
∵“m>a”是“函数$f(x)={(\frac{1}{3})^x}+m-\frac{1}{3}$的图象不过第三象限”的必要不充分条件,
∴实数a能取的最大整数为-1.
故选:D.
点评 本题考查了函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
5.关于x、y的方程组$\left\{\begin{array}{l}(m+1)x-y-3m=0\\ 4x+(m-1)y+7=0\end{array}\right.$( )
| A. | 有唯一的解 | B. | 有无穷多解 | ||
| C. | 由m的值决定解的情况 | D. | 无解 |
9.已知集合P={x|1<3x≤9},Q={1,2,3},则P∩Q=( )
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {1,2,3} |
4.已知集合A={1,3,5,7,9},B={1,3,9},则∁AB=( )
| A. | {5,7} | B. | {1,3,9} | C. | {3,5,7} | D. | {1,2,3} |
 已知F1、F2分别为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上、下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.
已知F1、F2分别为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上、下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.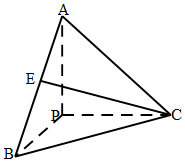 已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.
已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.