题目内容

11．下列函数既是偶函数，又在（0，+∞）上是增函数的是（　　）
A．y=x-2B．$y={x^{\frac{1}{3}}}$C．y=2|x|D．y=|x-1|+|x+1|

分析 逐一分析给定的四个函数的奇偶性和单调性，可得答案．

解答 解：函数y=x-2是偶函数，但在（0，+∞）上是减函数；
函数$y={x^{\frac{1}{3}}}$是奇函数，在（0，+∞）上是增函数；
函数y=2|x|=$\left\{\begin{array}{l}{2}^{-x}，x＜0\\{2}^{x}，x≥0\end{array}\right.$是偶函数，又在（0，+∞）上是增函数；
函数y=|x-1|+|x+1|=$\left\{\begin{array}{l}-2x，x＜-1\\ 2，-1≤x≤1\\ 2x，x＞1\end{array}\right.$是偶函数，但在（0，1]上不是增函数；
故选C

点评 本题考查的知识点是分段函数的应用，函数的奇偶性和函数的单调性，难度中档．

练习册系列答案
相关题目
1．已知△ABC中，a=5，b=4，C=60°，求：
（1）$\overrightarrow{BC}•\overrightarrow{CA}$；
（2）求|$\overrightarrow{AB}$|．
2．已知F1、F2分别为椭圆C1：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的上、下焦点，其中F1也是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|=$\frac{5}{3}$．
（I）求椭圆的方程；
（II）过抛物线C2上一点P（异于原点O）作切线l，交椭圆于A，B两点，Q是OP的中点，求△QAB面积的最大值．
19．在△ABC中，角A，B，C所对的边是a，b，c，且满足a2+c2-b2=ac．
（1）求角B的大小；
（2）设$\overrightarrow{m}$=（-3，-1），$\overrightarrow{n}$=（sinA，cos2A），求$\overrightarrow{m}$•$\overrightarrow{n}$的最小值．
6．已知圆O1：x2+y2=1与圆O2：（x+4）2+（y-a）2=25内切，则常数a=0．
16．过x轴上一点P作x轴的垂线，分别交函数y=sinx，y=cosx，y=tanx的图象于P1，P2，P3，若$\overrightarrow{P{P_3}}=\frac{3}{8}\overrightarrow{P{P_2}}$，则$|\overrightarrow{P{P_1}}|$=（　　）
A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{{\sqrt{3}}}{3}$D．$\frac{{2\sqrt{2}}}{3}$
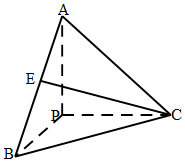3．已知如图，PA、PB、PC互相垂直，且长度相等，E为AB中点，则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$．
20．等差数列{an}中，a2=4，a4+a7=15．
（1）求数列{an}的通项公式；
（2）设bn=2an-2+n，求b1+b2+b3+…+b10的值．
1．方程x-sinx=0的根的个数为（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网