题目内容
已知函数f(x)=sin(ωx+
)(ω>0),若存在实数x0使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2013)成立,则ω的最小值是( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:显然要使结论成立,有f(x0)是最小值-1,f(x0+2013)是最大值1,当ω的最小时,函数的周期最大,故此时半个周期即为2013,由此求得ω的最小值.
解答:
解:显然要使结论成立,有f(x0)是最小值-1,f(x0+2013)是最大值1,
只需保证区间[x0,x0+2013]是半个周期,若是半个周期加一个周期的整数倍
当ω的最小时,函数的周期最大,故此时半个周期即为2013,即
•T=
×
=2013,
求得ω=
,
故选:A.
只需保证区间[x0,x0+2013]是半个周期,若是半个周期加一个周期的整数倍
当ω的最小时,函数的周期最大,故此时半个周期即为2013,即
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
求得ω=
| π |
| 2013 |
故选:A.
点评:本题主要考查函数y=Asin(ωx+φ)的图象特征,判断半个周期即为2013,是解题的关键,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知当|x|<
时,有
=1-2x+4x2-…+(-2x)n+…,根据以上信息,若对任意|x|<
,都有
=a0+a1x+a2x2+…+anxn+…,则a10= .
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
| x |
| (1-x3)(1+2x) |
已知奇函数y=f(x)在区间[-b,-a]上为减函数,且在此区间上,y=f(x)的最小值为2,则函数y=|f(x)|在区间[a,b]上是( )
| A、增函数且最大值为2 |
| B、增函数且最小值为2 |
| C、减函数且最大值为2 |
| D、减函数且最小值为2 |
下列说法错误的是( )
| A、数据1,2,3,4,5的平均数、众数、中位数都是3 | ||||||||
| B、若命题p∧q为真命,则p∨q为真 | ||||||||
| C、若p:?x∈R,x2-x+1>0,则¬p:?x0∈R,x02-x0+1≤0 | ||||||||
D、“若α=
|
执行如图的程序框图,则输出的S的值为( )


| A、1 | B、2 | C、3 | D、4 |
执行如图所示程序框图,则输出的S=( )


| A、-2014 | B、2014 |
| C、-2013 | D、2013 |
如图,在△ABC中,AB=1,AC=3,D是BC的中点,则
•
=( )
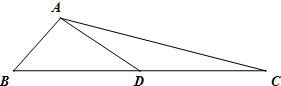
| AD |
| DC |

| A、3 | B、2 | C、5 | D、不确定 |
cos
+tan(-
)+sin21π的值为( )
| 9π |
| 4 |
| 7π |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图是甲、乙两名同学三次测验成绩的茎叶图,则甲、乙两名同学中成绩更稳定的是
如图是甲、乙两名同学三次测验成绩的茎叶图,则甲、乙两名同学中成绩更稳定的是