题目内容
已知Ω={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|x≥4,y≥0,x-2y≥0},若向区域Ω内随机投一点P,则点P落在区域A内的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:画出平面区域Ω的图形,求出区域Ω的面积,求出区域中满足A的面积,利用几何概型求出向Ω内随机投掷一点Q,则Q落在M内的概率.
解答:
 解:由题意画出平面区域Ω,以及A的区域,如图,
解:由题意画出平面区域Ω,以及A的区域,如图,
直线x+y≤6与x-2y≥0的交点坐标为(4,2),
所以区域Ω的面积是:
×6×6=18,
区域中A的面积为:
×2×2=2,
所求概率为P=
=
故选C.
 解:由题意画出平面区域Ω,以及A的区域,如图,
解:由题意画出平面区域Ω,以及A的区域,如图,直线x+y≤6与x-2y≥0的交点坐标为(4,2),
所以区域Ω的面积是:
| 1 |
| 2 |
区域中A的面积为:
| 1 |
| 2 |
所求概率为P=
| 2 |
| 18 |
| 1 |
| 9 |
故选C.
点评:本题考查几何概型的求法,注意区域的表示方法,考查线性规划问题,考查作图能力计算能力.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知当|x|<
时,有
=1-2x+4x2-…+(-2x)n+…,根据以上信息,若对任意|x|<
,都有
=a0+a1x+a2x2+…+anxn+…,则a10= .
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
| x |
| (1-x3)(1+2x) |
执行如图所示程序框图,则输出的S=( )


| A、-2014 | B、2014 |
| C、-2013 | D、2013 |
如图,在△ABC中,AB=1,AC=3,D是BC的中点,则
•
=( )
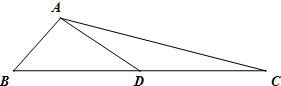
| AD |
| DC |

| A、3 | B、2 | C、5 | D、不确定 |
已知动点P(a,b)在不等式组
表示的平面区域内部运动,则
的取值范围是( )
|
| b+3 |
| a-1 |
A、(-
| ||
| B、(-3,2) | ||
C、(-∞,-
| ||
| D、(1,3) |
已知f(x)=x3-3x,则函数h(x)=f[f(x)]-1的零点个数是( )
| A、3 | B、5 | C、7 | D、9 |
把1100(2)化为十进制数,则此数为( )
| A、8 | B、12 | C、16 | D、20 |
cos
+tan(-
)+sin21π的值为( )
| 9π |
| 4 |
| 7π |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|