题目内容
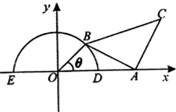 如图,半圆的圆心在直角坐标原点,点A,D,E的坐标分别为A(2,0),D(1,0),E(-1,0),且点B在半圆上自点D逆时针向点E运动,三角形ABC是等腰直角三形,∠BAC是直角,则四边形OACB的面积的最大值是( )
如图,半圆的圆心在直角坐标原点,点A,D,E的坐标分别为A(2,0),D(1,0),E(-1,0),且点B在半圆上自点D逆时针向点E运动,三角形ABC是等腰直角三形,∠BAC是直角,则四边形OACB的面积的最大值是( )A、
| ||||
B、2+2
| ||||
C、
| ||||
D、2+
|
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:利用余弦定理可求得AB2=5-4cosθ;于是S△ABC=
AB2=
-2cosθ,B(cosθ,sinθ),易求S△AOB=sinθ;四边形OACB的面积S=
-2cosθ+sinθ=
+
sin(θ+φ),从而可得答案.
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
解答:
解:设∠BOA=θ,由余弦定理得,AB2=OB2+OA2-2OB•OAcosθ=1+4-2×1×2cosθ=5-4cosθ;
∵三角形ABC是等腰直角三形,∠BAC是直角,
∴S△ABC=
AB2=
-2cosθ;
又B(cosθ,sinθ),
∴S△AOB=
×OA×sinθ=
×2sinθ=sinθ;
∴四边形OACB的面积S=
-2cosθ+sinθ=
+
sin(θ+φ)(其中tanφ=-2),
∴Smax=
+
,
故选:A.
∵三角形ABC是等腰直角三形,∠BAC是直角,
∴S△ABC=
| 1 |
| 2 |
| 5 |
| 2 |
又B(cosθ,sinθ),
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形OACB的面积S=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
∴Smax=
| 5 |
| 2 |
| 5 |
故选:A.
点评:本题考查任意角的三角函数的定义,求得四边形OACB的面积S=
+
sin(θ+φ)是关键,着重考查余弦定理与辅助角公式的应用,考查三角函数的最值,属于中档题.
| 5 |
| 2 |
| 5 |

练习册系列答案
相关题目
下列说法错误的是( )
| A、数据1,2,3,4,5的平均数、众数、中位数都是3 | ||||||||
| B、若命题p∧q为真命,则p∨q为真 | ||||||||
| C、若p:?x∈R,x2-x+1>0,则¬p:?x0∈R,x02-x0+1≤0 | ||||||||
D、“若α=
|
执行如图所示程序框图,则输出的S=( )


| A、-2014 | B、2014 |
| C、-2013 | D、2013 |
“m=2”是“直线l1:mx+4y-6=0与直线l2:x+my-3=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如图,在△ABC中,AB=1,AC=3,D是BC的中点,则
•
=( )
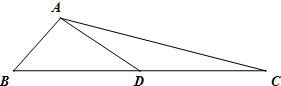
| AD |
| DC |

| A、3 | B、2 | C、5 | D、不确定 |
已知动点P(a,b)在不等式组
表示的平面区域内部运动,则
的取值范围是( )
|
| b+3 |
| a-1 |
A、(-
| ||
| B、(-3,2) | ||
C、(-∞,-
| ||
| D、(1,3) |
把1100(2)化为十进制数,则此数为( )
| A、8 | B、12 | C、16 | D、20 |