题目内容

在△ABC中，若|
BA
+
BC
|=|
AC
|，则△ABC的形状为
 
．
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：利用向量加法的平行四边形法则，得到
BA
+
BC
=
BD
，又由|
BA
+
BC
|=|
AC
|，则向量
BA
，
BC
夹角直角，故得三角形为直角三角形．．
解答： 解：以BA，BC为邻边建立平行四边形ABCD，
则
BA
+
BC
=
BD
，
又由|
BA
+
BC
|=|
AC
|，
则平行四边形ABCD为矩形
∴
BA
⊥
BC
，
∴∠B=90°，故△ABC为直角三角形．
故答案为：直角三角形．
点评：本题考查数量积的化简运算及向量的加法运算，特别是三角形相邻两边向量之和问题．
练习册系列答案
相关题目
已知命题：“?x∈[-2，1]，使x2+2x+a≥0”为真命题，则a的取值范围是
 
．
如图是甲、乙两名同学三次测验成绩的茎叶图，则甲、乙两名同学中成绩更稳定的是
 
．（填“甲”或“乙”）
已知点A（4，2），F为抛物线y2=8x的焦点，点M在抛物线上移动，当|MA|+|MF|取最小值时，M点的坐标为
 
．
若点P（x，y）在曲线
x=1+
5
sinθ
y=4+
5
cosθ
（θ为参数，θ∈R）上，则
x+2
y
的取值范围是
 
．
下列各数210（6），100（4），111111（2）中最小的数是
 
．
已知当|x|＜
1
2
时，有
1
1+2x
=1-2x+4x2-…+（-2x）n+…，根据以上信息，若对任意|x|＜
1
2
，都有
x
(1-x3)(1+2x)
=a0+a1x+a2x2+…+anxn+…，则a10=
 
．
已知奇函数y=f（x）在区间[-b，-a]上为减函数，且在此区间上，y=f（x）的最小值为2，则函数y=|f（x）|在区间[a，b]上是（　　）
A、增函数且最大值为2
B、增函数且最小值为2
C、减函数且最大值为2
D、减函数且最小值为2
如图，在△ABC中，AB=1，AC=3，D是BC的中点，则
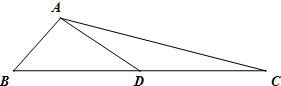
AD
•
DC
=（　　）
A、3B、2C、5D、不确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网