题目内容
已知集合A={x|(x-1)(x-4)>0},B={x|log2x<1},则集合(∁RA)∩B=( )
| A、{x|1≤x≤4} |
| B、{x|0<x<2} |
| C、{x|1≤x<2} |
| D、{x|2<x≤4} |
考点:交、并、补集的混合运算
专题:集合
分析:解一元二次不等式求得A,可得(∁RA,解对数不等式求得B,再根据两个集合的交集的定义求得(∁RA)∩B.
解答:
解:∵集合A={x|(x-1)(x-4)>0}={x|x<1,或 x>4},
∴∁RA={x|1≤x≤4}.
又B={x|log2x<1}={x|0<x<2},
∴(∁RA)∩B={x|1≤x<2},
故选:C.
∴∁RA={x|1≤x≤4}.
又B={x|log2x<1}={x|0<x<2},
∴(∁RA)∩B={x|1≤x<2},
故选:C.
点评:本题主要考查一元二次不等式、对数不等式的解法,求集合的补集,两个集合的交集的定义和求法,属于基础题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知奇函数y=f(x)在区间[-b,-a]上为减函数,且在此区间上,y=f(x)的最小值为2,则函数y=|f(x)|在区间[a,b]上是( )
| A、增函数且最大值为2 |
| B、增函数且最小值为2 |
| C、减函数且最大值为2 |
| D、减函数且最小值为2 |
执行如图的程序框图,则输出的S的值为( )


| A、1 | B、2 | C、3 | D、4 |
执行如图所示程序框图,则输出的S=( )


| A、-2014 | B、2014 |
| C、-2013 | D、2013 |
物体自由落体运动方程为s(t)=
gt2,若
=g=9.8m/s,那么下面说法正确的是( )
| 1 |
| 2 |
| lim |
| n→∞ |
| s(1+△t)-s(1) |
| △t |
| A、9.8m/s是0~1s这段时间内的平均速度 |
| B、9.8m/s是从1s到(1+△t)s这段时间内的速度 |
| C、9.8m/s是物体在t=1s这一时刻的速度 |
| D、9.8m/s是物体从1s到(1+△t)s这段时间内的平均速度 |
如图,在△ABC中,AB=1,AC=3,D是BC的中点,则
•
=( )
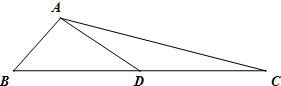
| AD |
| DC |

| A、3 | B、2 | C、5 | D、不确定 |
已知f(x)=x3-3x,则函数h(x)=f[f(x)]-1的零点个数是( )
| A、3 | B、5 | C、7 | D、9 |
已知x,y之间的数据如下表所示,则y与x之间的线性回归方程必过点( )
| x | 1.08 | 1.12 | 1.19 | 1.30 |
| y | 2.25 | 2.37 | 2.40 | 2.60 |
| A、(0,0) |
| B、(1.17,0) |
| C、(0,2.41) |
| D、(1.17,2.41) |