题目内容
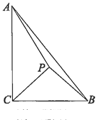 如图,在Rt△ABC中,∠ACB=
如图,在Rt△ABC中,∠ACB=| π |
| 2 |
(1)若P是等腰三角形PBC的直角顶角,求PA的长;
(2)若∠BPC=
| 2π |
| 3 |
考点:余弦定理,两角和与差的余弦函数,两角和与差的正弦函数,正弦定理
专题:解三角形
分析:(1)由三角形PBC为等腰直角三角形,利用勾股定理求出PC的长,在三角形PAC中,利用余弦定理求出PA的长即可;
(2)在三角形PBC中,由∠BPC与∠PCB的度数表示出∠PBC的度数,利用正弦定理表示出PB与PC,进而表示出三角形PBC面积,利用正弦函数的值域确定出面积的最大值即可.
(2)在三角形PBC中,由∠BPC与∠PCB的度数表示出∠PBC的度数,利用正弦定理表示出PB与PC,进而表示出三角形PBC面积,利用正弦函数的值域确定出面积的最大值即可.
解答:
解:(1)∵P为等腰直角三角形PBC的直角顶点,且BC=2,
∴∠PCB=
,PC=
,
∵∠ACB=
,∴∠ACP=
,
在△PAC中,由余弦定理得:PA2=AC2+PC2-2AC•PC•cos
=5,
整理得:PA=
;
(2)在△PBC中,∠BPC=
,∠PCB=θ,
∴∠PBC=
-θ,
由正弦定理得:
=
=
,
∴PB=
sinθ,PC=
sin(
-θ),
∴△PBC的面积S(θ)=
PB•PCsin
=
sin(
-θ)sinθ=
sin(2θ+
)-
,θ∈(0,
),
则当θ=
时,△PBC面积的最大值为
.
∴∠PCB=
| π |
| 4 |
| 2 |
∵∠ACB=
| π |
| 2 |
| π |
| 4 |
在△PAC中,由余弦定理得:PA2=AC2+PC2-2AC•PC•cos
| π |
| 4 |
整理得:PA=
| 5 |
(2)在△PBC中,∠BPC=
| 2π |
| 3 |
∴∠PBC=
| π |
| 3 |
由正弦定理得:
| 2 | ||
sin
|
| PB |
| sinθ |
| PC | ||
sin(
|
∴PB=
4
| ||
| 3 |
4
| ||
| 3 |
| π |
| 3 |
∴△PBC的面积S(θ)=
| 1 |
| 2 |
| 2π |
| 3 |
4
| ||
| 3 |
| π |
| 3 |
2
| ||
| 3 |
| π |
| 6 |
| ||
| 3 |
| π |
| 3 |
则当θ=
| π |
| 6 |
| ||
| 3 |
点评:此题考查了正弦、余弦定理,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线y=ex与直线y=5-x交点的纵坐标在区间(m,m+1)(m∈Z)内,则实数m的值为( )
| A、1 | B、2 | C、3 | D、4' |
设等差数列{an}的前n项和为Sn,若a2=-11,a5+a9=-2,则当Sn取最小值时,n等于( )
| A、9 | B、8 | C、7 | D、6 |
若a≠b,则等差数列a,x1,x2,b的公差是( )
| A、b-a | ||
B、
| ||
C、
| ||
D、
|